Sliding Window Maximum

LeetCode #239 [Hard]

Problem Statement

Given an array and window size k, find the maximum value in each sliding window of size k.

Example: nums = [1,3,-1,-3,5,3,6,7], k=3 → Output: [3,3,5,5,6,7]

Approach 1: Brute Force

Explanation: For each window, scan all elements to find maximum.

Time Complexity: O(n*k)

Space Complexity: O(n) for output

result = []
for i in 0..n-k:
    max_val = max(nums[i..i+k-1])
    result.append(max_val)
return result
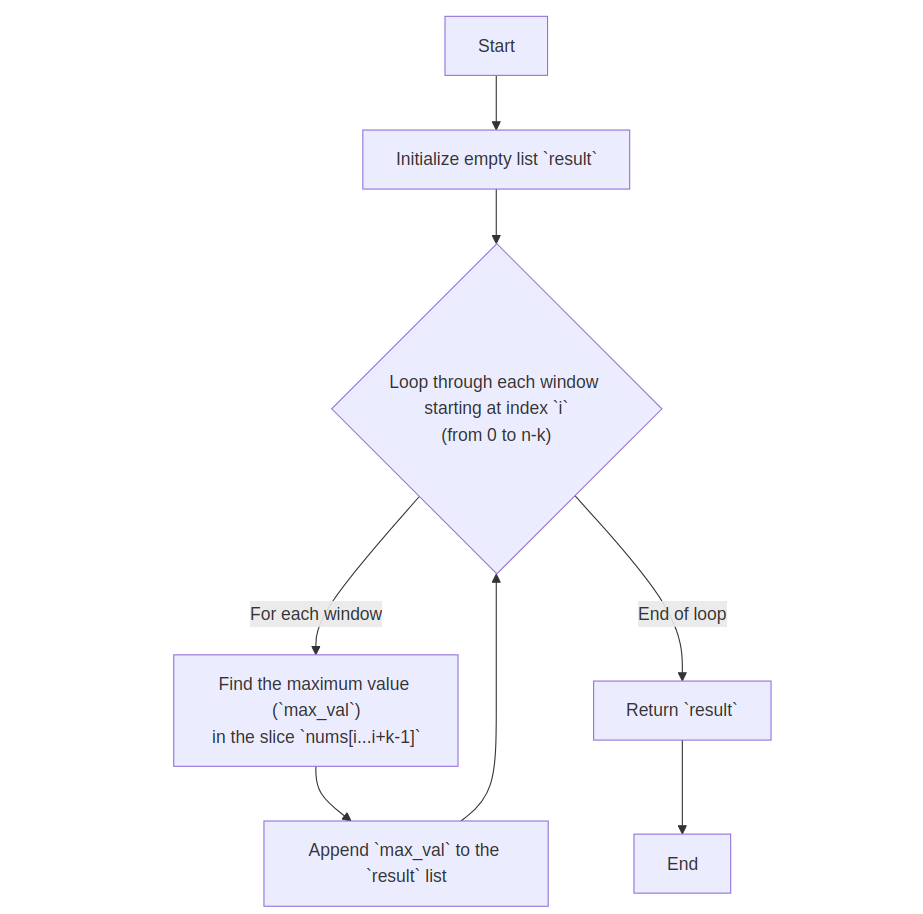
Heap Sort Flowchart

💡 Think: Compute a max for each window by full scan.

Approach 2: Using Deque (Better)

Explanation: Maintain deque of indices in decreasing order; front is max.

Time Complexity: O(n)

Space Complexity: O(k)

deque = empty
result = []
for i in 0..n-1:
    while deque not empty and nums[deque[-1]] < nums[i]:
        deque.pop()
    deque.push(i)
    if deque[0] == i-k:
        deque.popleft()
    if i >= k-1:
        result.append(nums[deque[0]])
return result
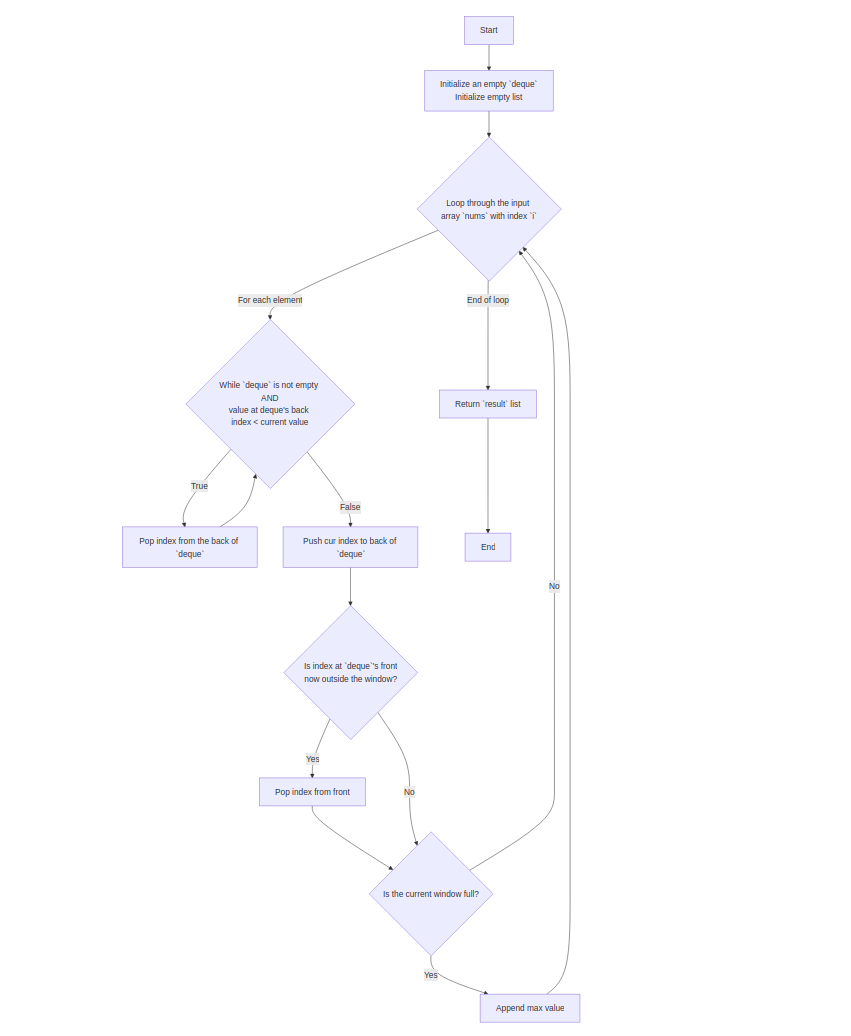
Heap Sort Flowchart

💡 Think: Keep a decreasing deque of indices; front is window max.

Approach 3: Max-Heap (Alternative)

Explanation: Keep a max-heap of window elements.

Time Complexity: O(n log k)

Space Complexity: O(k)

heap = max-heap of first k elements
result = [heap.max()]
for i in k..n-1:
    remove nums[i-k] from heap
    insert nums[i] into heap
    result.append(heap.max())
return result
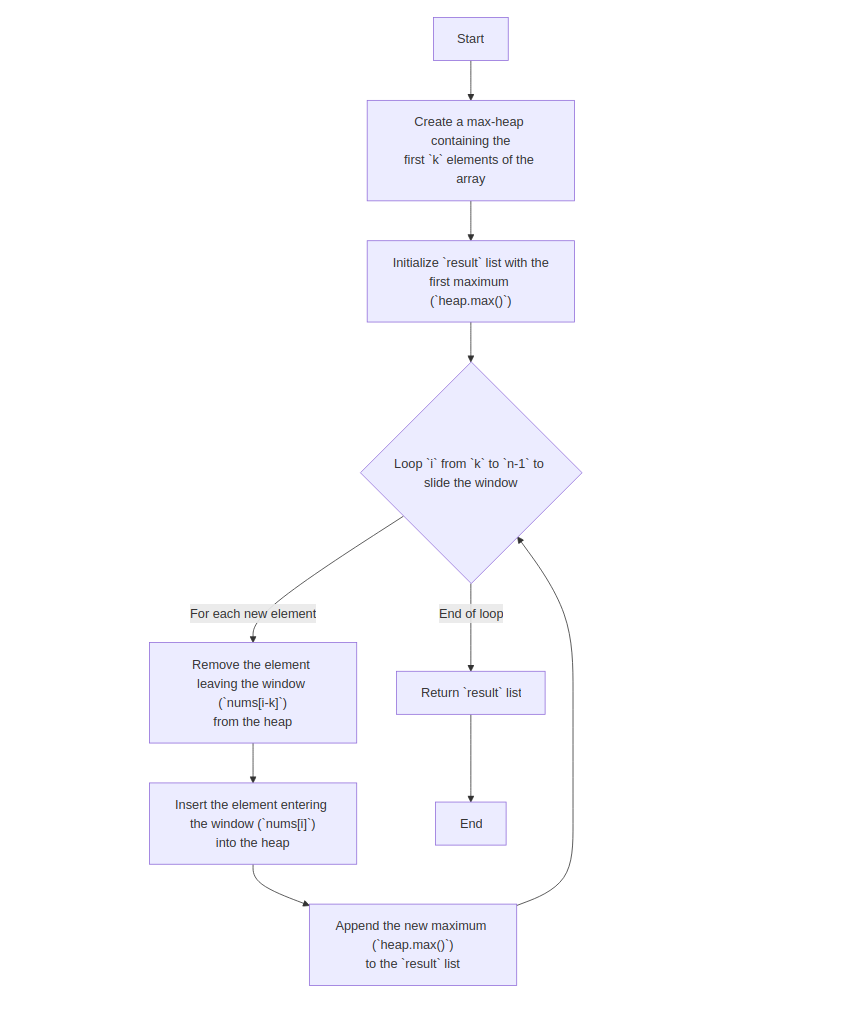
Heap Sort Flowchart

💡 Think: Maintain a heap of window values; discard out-of-window entries.

Solve on LeetCode