Min Stack

Problem Statement

Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.

Example: push(2), push(0), push(3), push(0), getMin() → 0

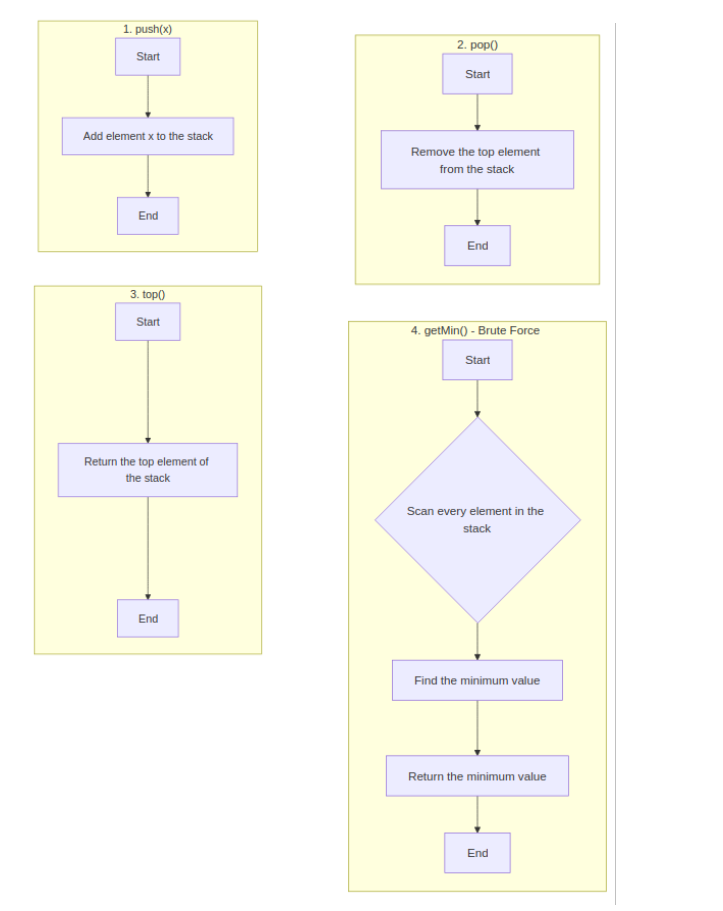
Approach 1: Brute Force

Explanation: Store all elements; find min by scanning stack each time.

Time Complexity: push/pop O(1), getMin O(n)

Space Complexity: O(n)

stack = empty
push(x): stack.push(x)
pop(): stack.pop()
top(): return stack[-1]
getMin(): return min(stack)

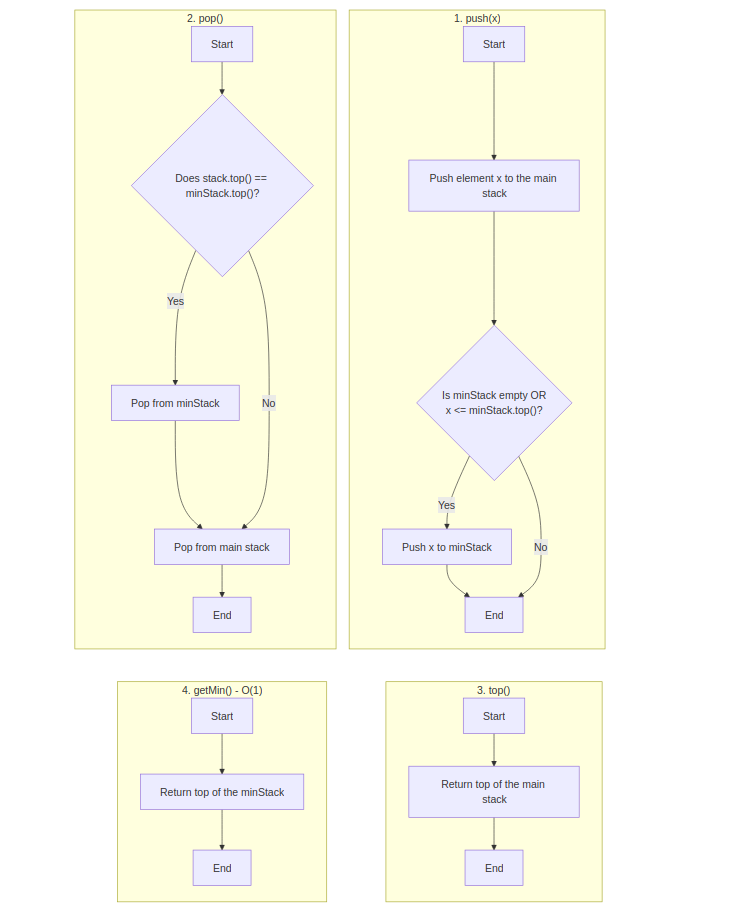
Approach 2: Auxiliary Stack (Better)

Explanation: Maintain an additional stack to track current minimum.

Time Complexity: O(1) for all operations

Space Complexity: O(n)

stack = empty
minStack = empty
push(x):
    stack.push(x)
    if minStack is empty or x <= minStack.top():
        minStack.push(x)
pop():
    if stack.pop() == minStack.top():
        minStack.pop()
top(): return stack.top()
getMin(): return minStack.top()

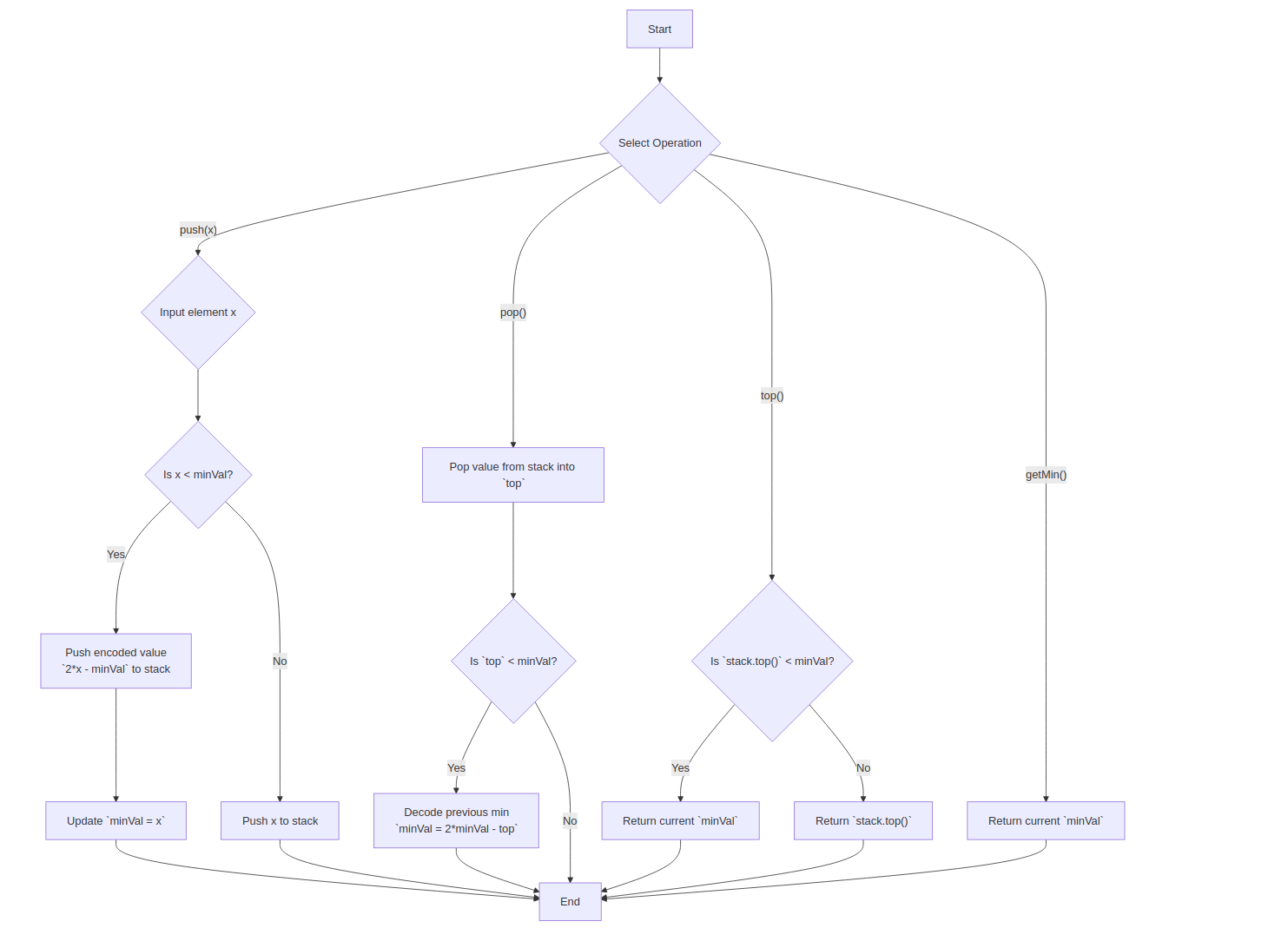
Approach 3: Single Stack with Encoded Values (Optimal)

Explanation: Use single stack with encoded differences to track minimum.

Time Complexity: O(1)

Space Complexity: O(n)

stack = empty
minVal = ∞
push(x):
    if x < minVal:
        stack.push(2*x - minVal)
        minVal = x
    else:
        stack.push(x)
pop():
    top = stack.pop()
    if top < minVal:
        minVal = 2*minVal - top
top(): return minVal if top < minVal else top
getMin(): return minVal