Infix To Postfix Conversion

GeeksforGeeks [Medium]

Problem Statement

Convert a given infix expression (e.g., (A+B)*C) into its postfix form (e.g., AB+C*) using a stack.

Example: (A+B)*C → AB+C*

Approach 1: Simple Stack Traversal

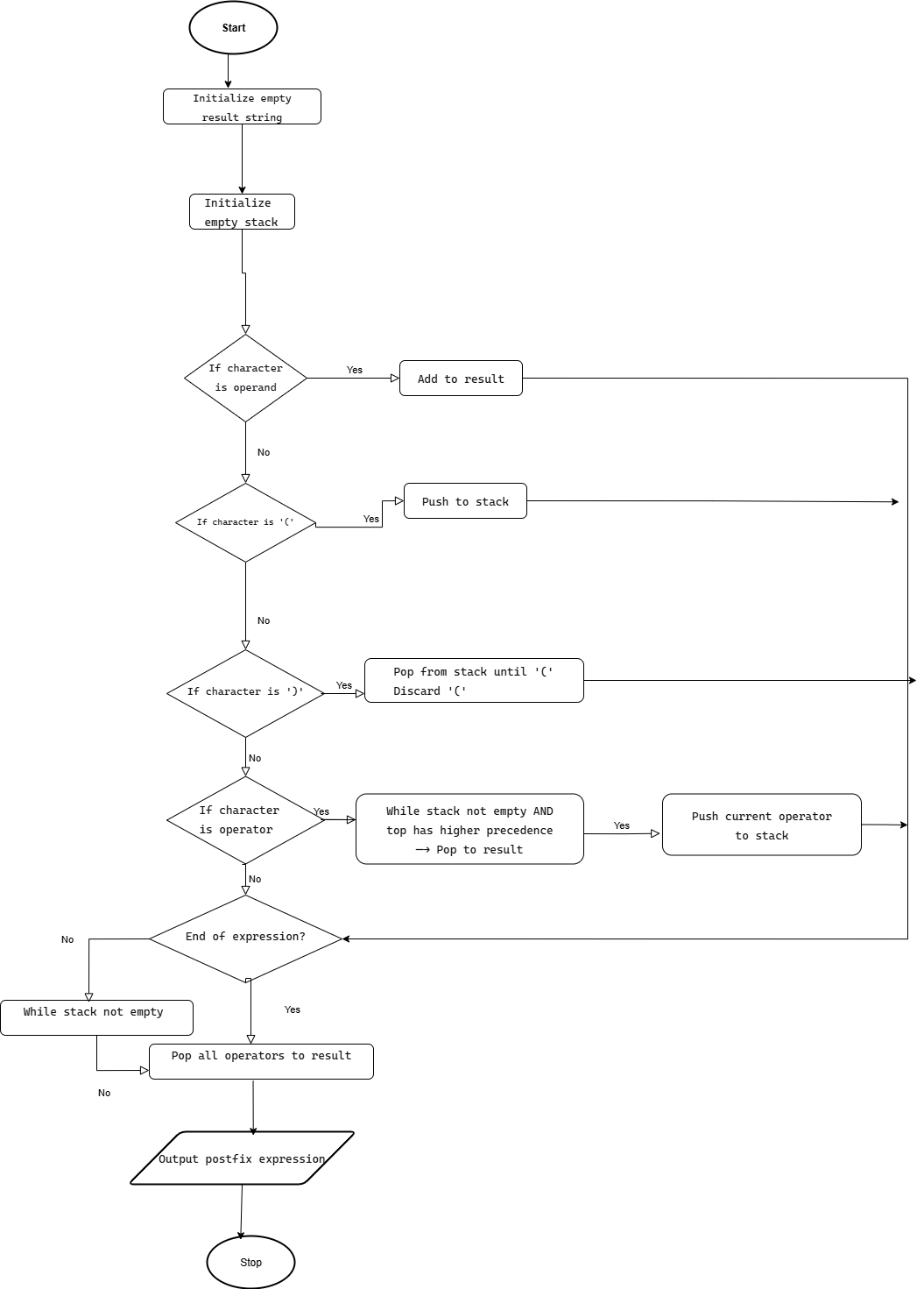
Explanation: Traverse the infix expression, push operators to stack, append operands to output. Pop operators based on precedence and parentheses.

Time Complexity: O(n)

Space Complexity: O(n)

stack = empty
result = ""
for each character c in expression:
    if c is operand:
        append c to result
    else if c is '(':
        push c to stack
    else if c is ')':
        pop until '(' and append to result
    else if c is operator:
        while top of stack has higher precedence:
            pop and append to result
        push c to stack
pop remaining operators and append to result
Flowchart Approach 1

💡 Think: Use a stack to store operators and append operands directly to the output.

Approach 2: Handle Multi-Character Operands (Better)

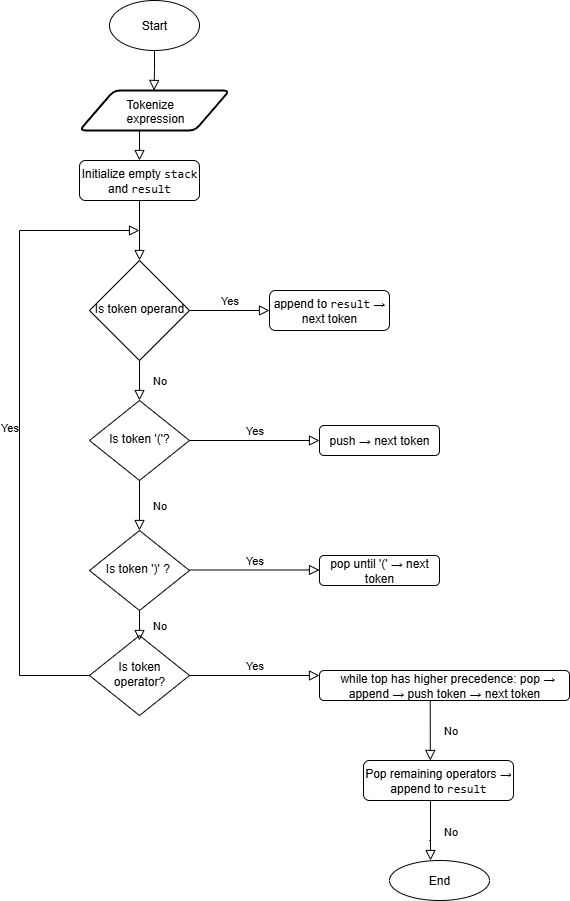
Explanation: Tokenize the expression to support multi-character operands, then apply same stack-based algorithm.

Time Complexity: O(n)

Space Complexity: O(n)

tokens = tokenize(expression)
stack = empty
result = ""
for each token:
    if token is operand:
        append token to result
    else if token is '(':
        push token
    else if token is ')':
        pop until '(' and append to result
    else if token is operator:
        while top has higher precedence:
            pop and append to result
        push token
pop remaining operators
Flowchart Approach 2

💡 Think: Pop from the stack when an operator of higher or equal precedence is found before pushing the new one.

Approach 3: Optimized Stack with Precedence Map (Optimal)

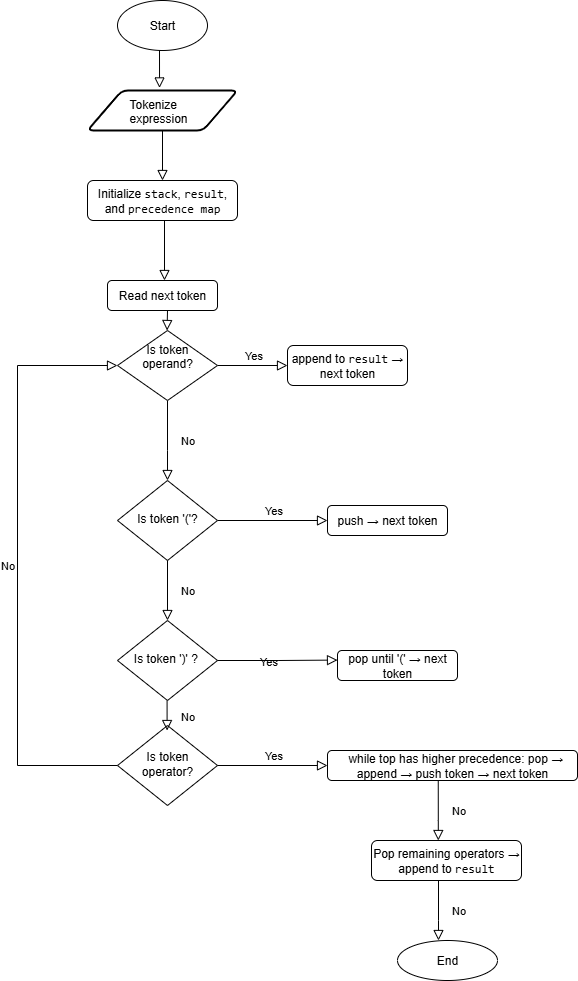
Explanation: Use a precedence map for operators to efficiently decide when to pop stack elements.

Time Complexity: O(n)

Space Complexity: O(n)

precedence = {'+':1, '-':1, '*':2, '/':2, '^':3}
stack = empty
result = ""
for each token:
    if token is operand:
        append to result
    else if token is '(':
        push to stack
    else if token is ')':
        pop until '('
    else if token is operator:
        while stack not empty and precedence[top] >= precedence[token]:
            pop and append to result
        push token
pop remaining operators
Flowchart Approach 3

💡 Think: Handle parentheses by pushing '(' and popping until '(' when ')' appears.

Solve on LeetCode