Topological Sort

Problem Statement

Return a topological ordering of a Directed Acyclic Graph (DAG).

Example: Graph with edges [[5,2],[5,0],[4,0],[4,1],[2,3],[3,1]] → [5,4,2,3,1,0]

Approach 1: DFS Post-order

Explanation: Perform DFS and add nodes to stack after exploring neighbors; reverse stack gives order.

Time Complexity: O(V + E)

Space Complexity: O(V) recursion stack

visited = set()
stack = []
function DFS(node):
    visited.add(node)
    for neighbor in node.neighbors:
        if neighbor not visited:
            DFS(neighbor)
    stack.push(node)
for node in all_nodes:
    if node not visited:
        DFS(node)
return reversed(stack)

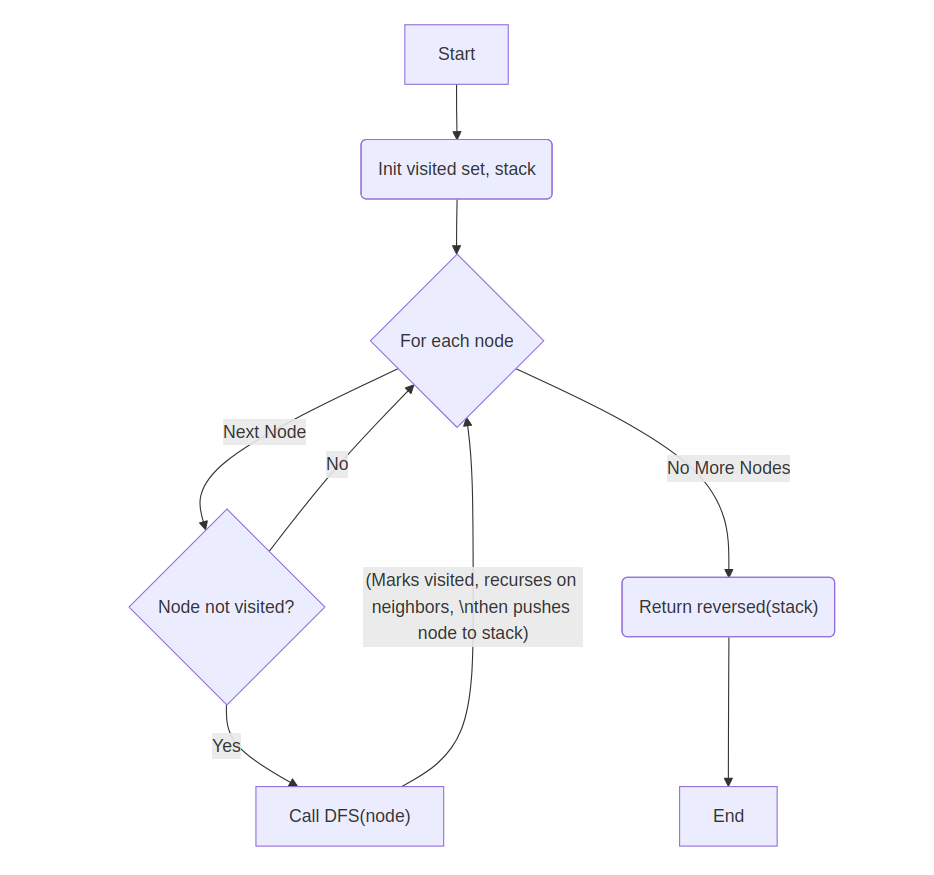
💡 Think: Finish times matter—push after exploring neighbors; reverse the stack for order.

Approach 2: Kahn’s Algorithm (BFS)

Explanation: Use in-degree array; push nodes with 0 in-degree into queue and update in-degrees.

Time Complexity: O(V + E)

Space Complexity: O(V)

in_degree = [0]*V
for u in all_nodes:
    for v in u.neighbors:
        in_degree[v] += 1
queue = nodes with in_degree 0
while queue not empty:
    node = queue.pop()
    result.append(node)
    for neighbor in node.neighbors:
        in_degree[neighbor] -= 1
        if in_degree[neighbor]==0:
            queue.push(neighbor)
return result

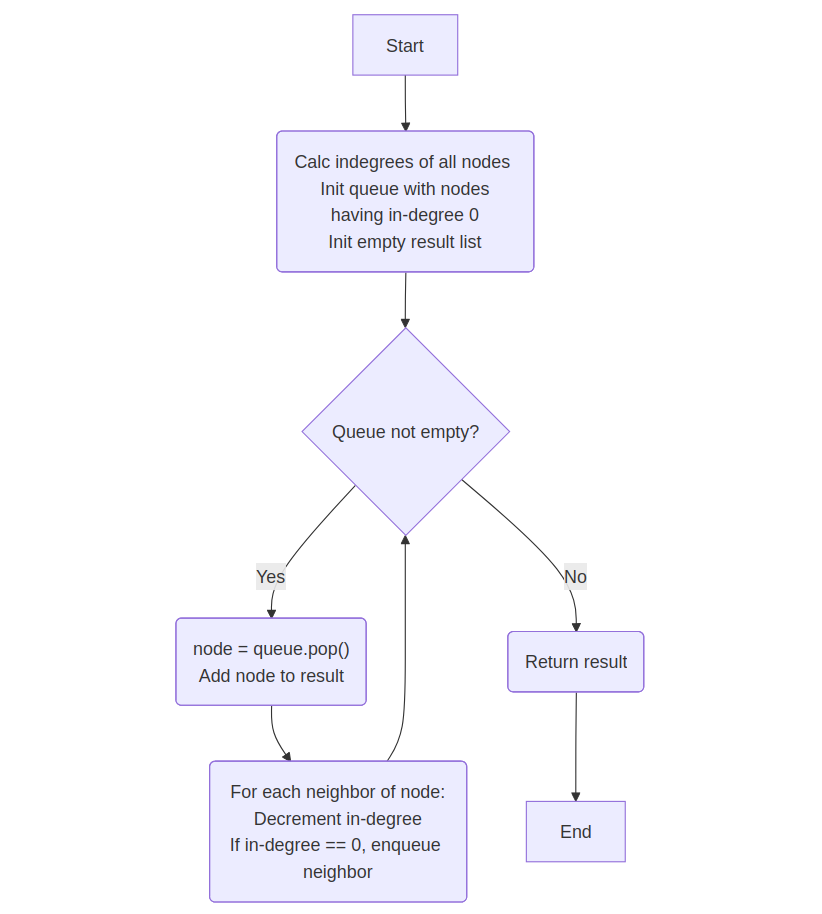
💡 Think: Peel nodes with in-degree 0 using a queue, decreasing in-degrees as edges are removed.

Solve on LeetCode