Minimum Spanning Tree (MST)

LeetCode #1584 [Medium]

Problem Statement

Find a tree connecting all nodes with minimum total edge weight in a connected undirected graph.

Example: Graph edges = [[0,1,4],[0,2,3],[1,2,1],[1,3,2],[2,3,4]] → MST total weight = 7

Approach 1: Kruskal’s Algorithm

Explanation: Sort edges by weight, add to MST if it doesn’t form cycle using Union-Find.

Time Complexity: O(E log E)

Space Complexity: O(V)

sort edges by weight
parent = [i for i in range(V)]
function find(x):
    if parent[x] != x: parent[x] = find(parent[x])
    return parent[x]
function union(x,y):
    parent[find(x)] = find(y)
mst_weight = 0
for edge(u,v,w) in sorted edges:
    if find(u) != find(v):
        union(u,v)
        mst_weight += w
return mst_weight
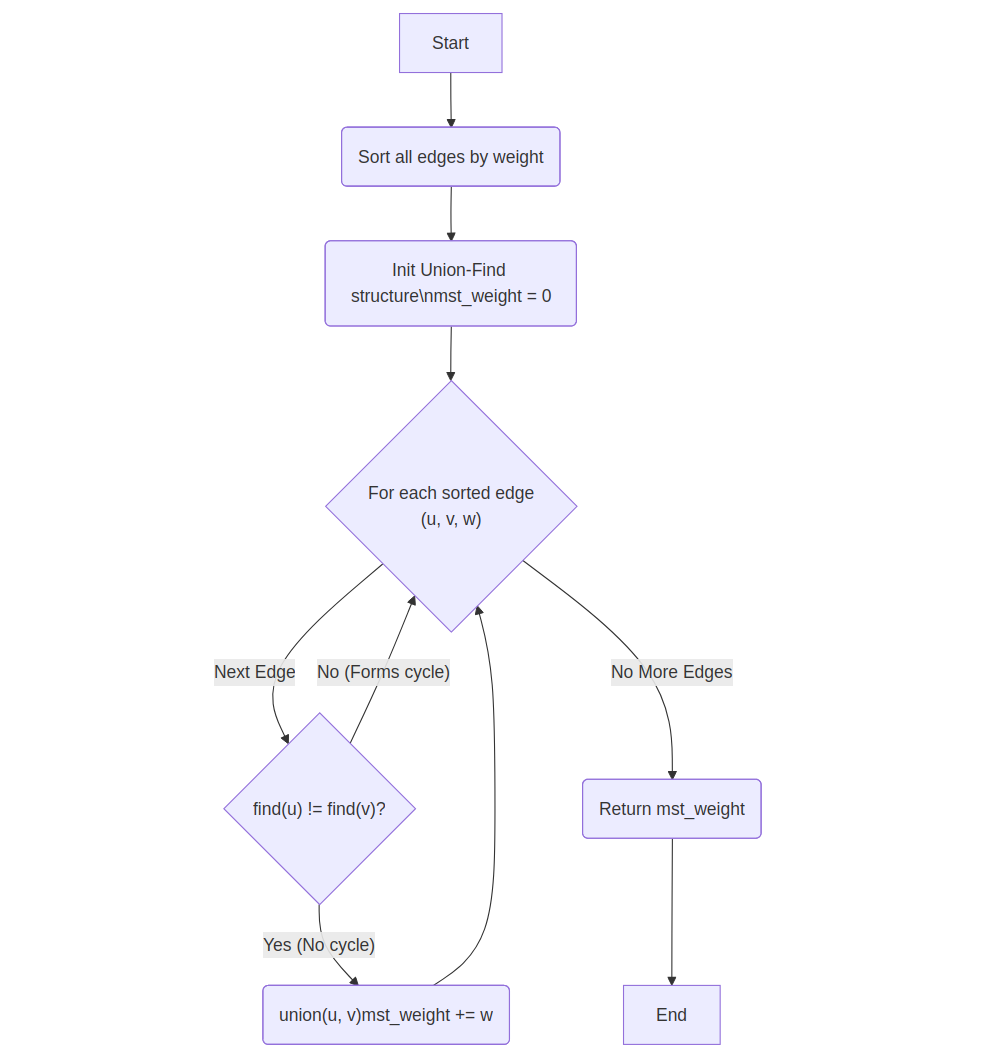
Heap Sort Flowchart

💡 Think: Sort edges; add the next lightest that doesn't form a cycle using DSU.

Approach 2: Prim’s Algorithm

Explanation: Start from a node, iteratively add smallest edge connecting MST to remaining nodes using min-heap.

Time Complexity: O(E log V)

Space Complexity: O(V + E)

visited = set()
min_heap = [(0, start_node)]
mst_weight = 0
while min_heap not empty:
    (weight, node) = heap.pop()
    if node in visited: continue
    visited.add(node)
    mst_weight += weight
    for neighbor, w in node.neighbors:
        if neighbor not in visited:
            heap.push((w, neighbor))
return mst_weight
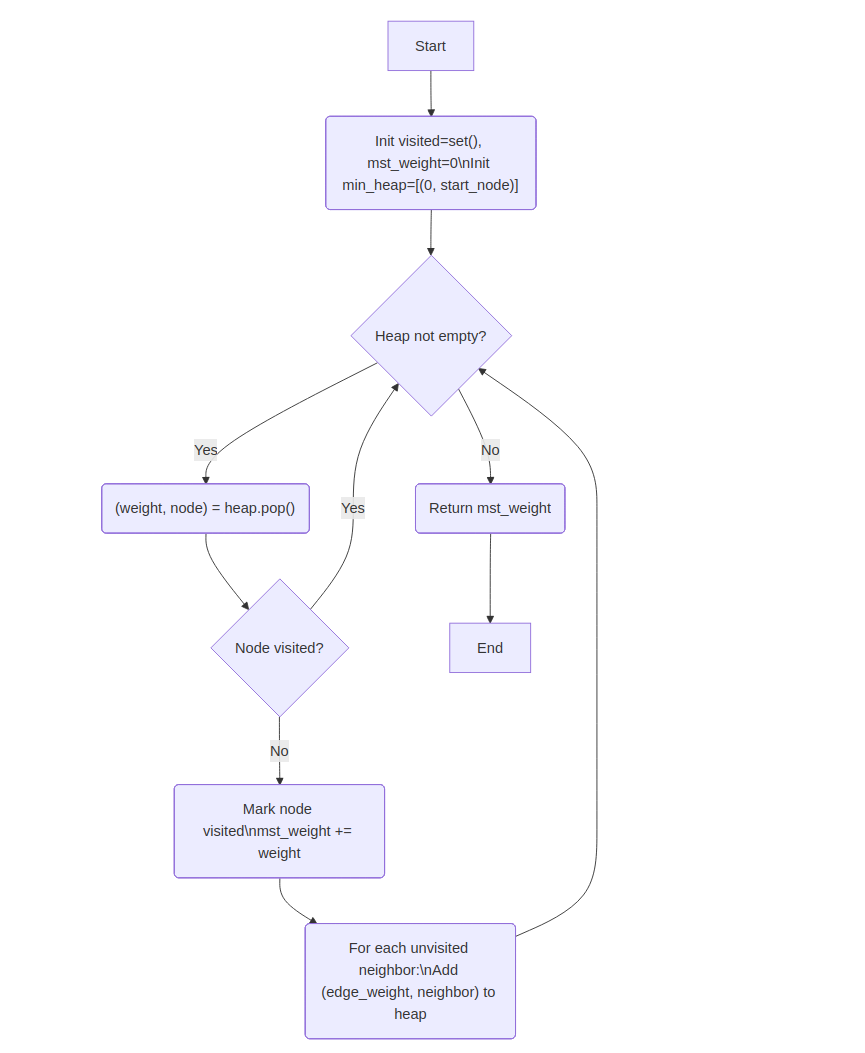
Heap Sort Flowchart

💡 Think: Grow from any node; pick the cheapest edge to a new node using a min-heap.

Solve on LeetCode