BFS & DFS Traversals

Problem Statement

Given a graph, traverse all nodes using BFS and DFS starting from a given node.

Example: Graph: 0→1,0→2,1→2,2→0,2→3 → BFS(0) = [0,1,2,3], DFS(0) = [0,1,2,3]

Approach 1: BFS (Queue)

Explanation: Use a queue to explore nodes level by level.

Time Complexity: O(V + E)

Space Complexity: O(V)

queue = [start]
visited[start] = true
while queue not empty:
    node = queue.pop()
    for neighbor in node.neighbors:
        if neighbor not visited:
            queue.push(neighbor)
            visited[neighbor] = true

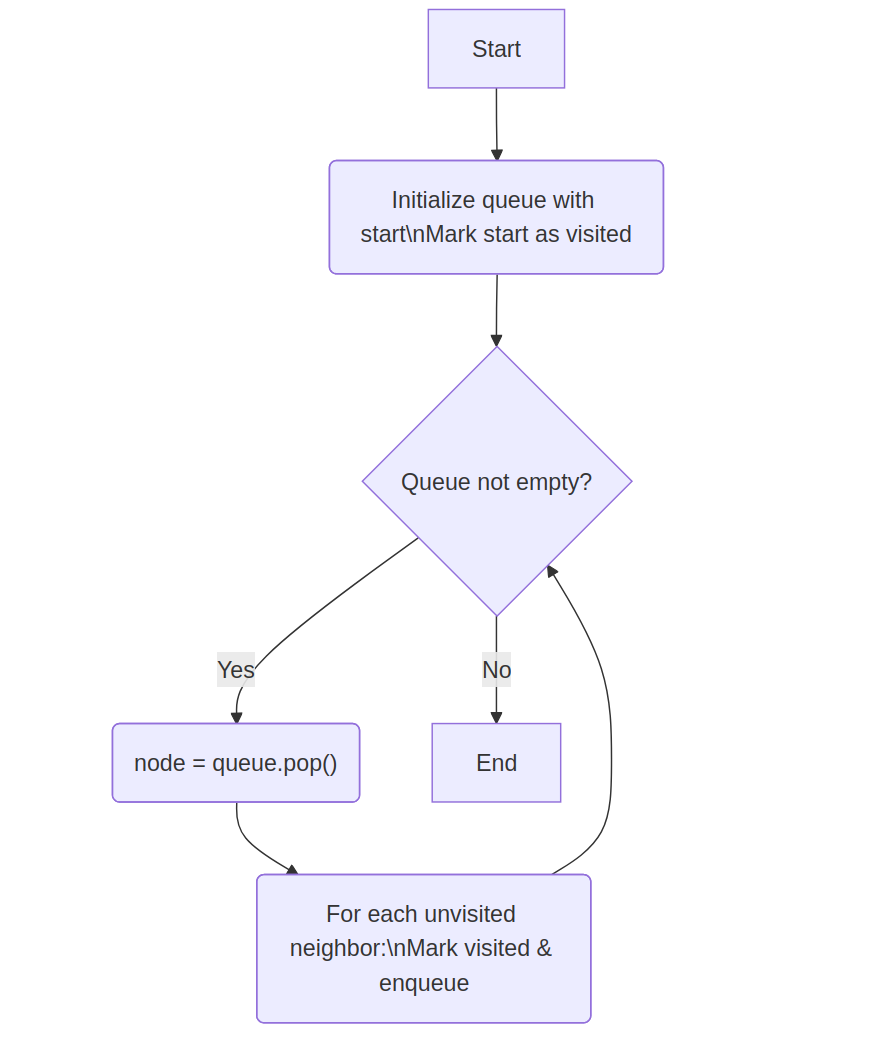
💡 Think: Explore level by level using a queue; enqueue unseen neighbors as you go.

Approach 2: DFS (Recursive)

Explanation: Recursively visit neighbors using a visited set.

Time Complexity: O(V + E)

Space Complexity: O(V) (recursion stack)

function DFS(node):
    visited[node] = true
    for neighbor in node.neighbors:
        if neighbor not visited:
            DFS(neighbor)
DFS(start)

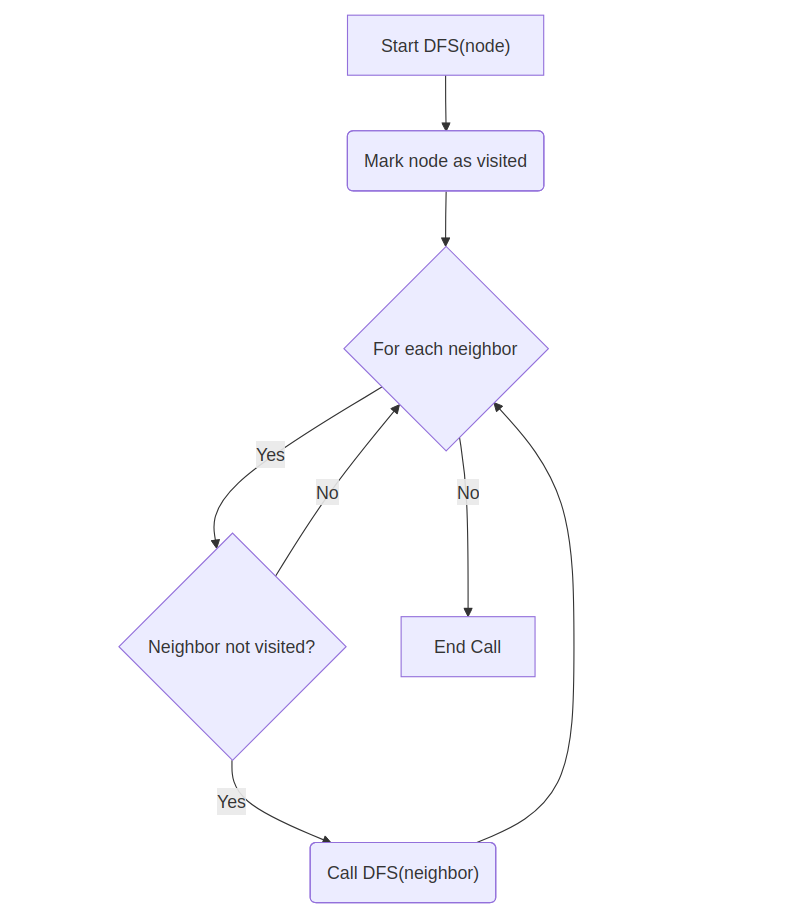
💡 Think: Dive deep along one path via recursion, backtrack when stuck using a visited set.

Approach 3: DFS (Iterative)

Explanation: Use a stack to simulate recursion.

Time Complexity: O(V + E)

Space Complexity: O(V)

stack = [start]
visited[start] = true
while stack not empty:
    node = stack.pop()
    for neighbor in node.neighbors:
        if neighbor not visited:
            stack.push(neighbor)
            visited[neighbor] = true

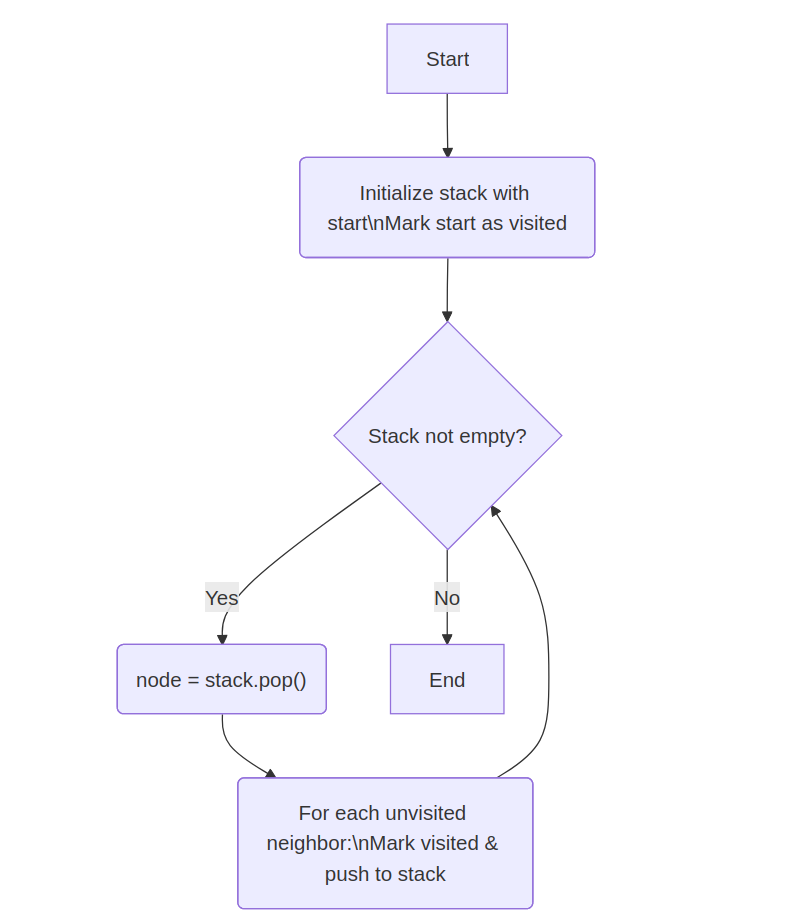
💡 Think: Use an explicit stack to mimic recursion, pushing neighbors and exploring depth-first.

Solve on LeetCode