Unbounded Knapsack

Problem Statement

Given n items with weights wt[] and values val[], and a knapsack capacity W, determine the maximum total value you can obtain. You can use **each item multiple times**.

Example: Input: W = 8, wt = [2,3,5], val = [50,100,140], Output: 300 (take two 3-weight items and one 2-weight)

Approach 1: Recursion

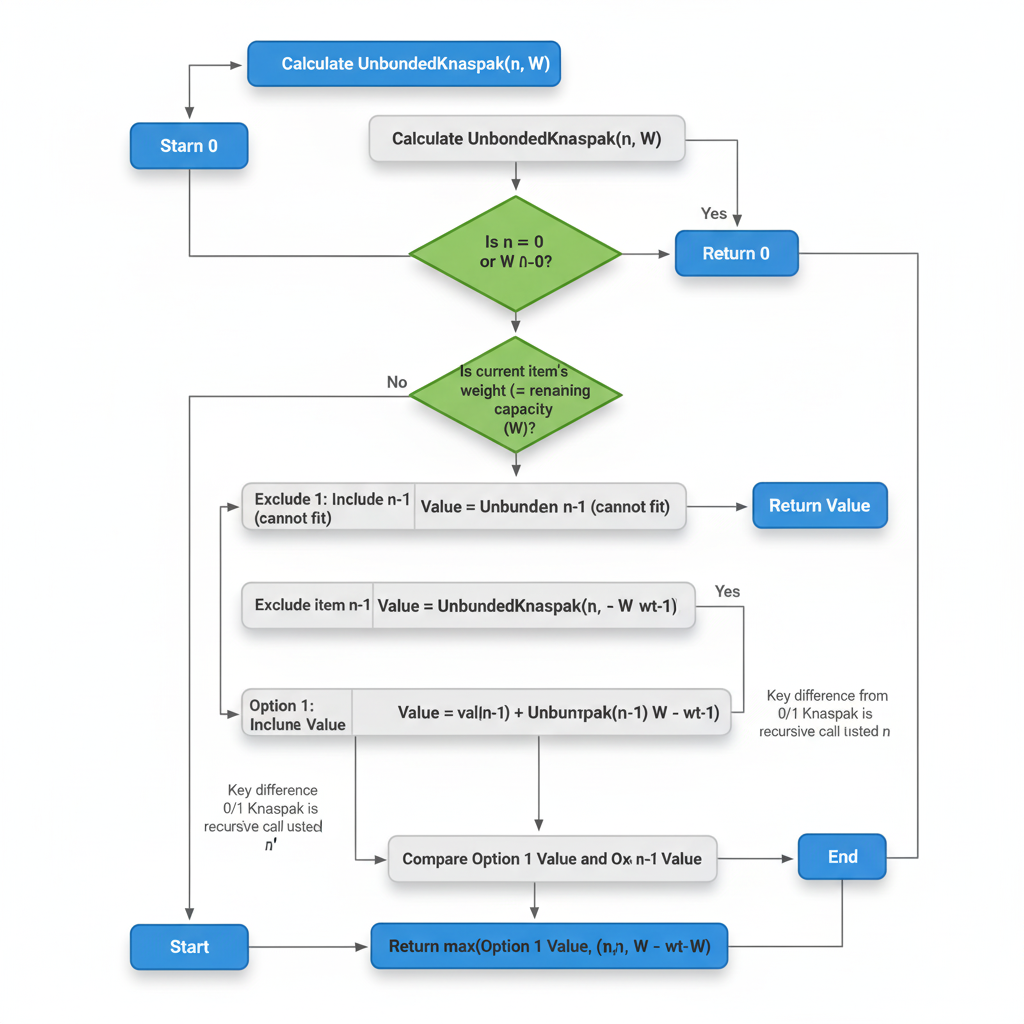
Explanation: For each item, decide how many times to include it (0 to W/wt[i]) recursively.

Time Complexity: Exponential

Space Complexity: O(n) recursion stack

function UnboundedKnapsack(W, n):
    if n == 0 or W == 0: return 0
    if wt[n-1] <= W:
        return max(
            val[n-1] + UnboundedKnapsack(W - wt[n-1], n),
            UnboundedKnapsack(W, n-1)
        )
    else:
        return UnboundedKnapsack(W, n-1)

💡 Think: Allow reusing an item by staying on the same i when you include it.

Approach 2: Memoization (Top-Down DP)

Explanation: Store results for subproblems (W, n) to avoid recomputation.

Time Complexity: O(n * W)

Space Complexity: O(n * W) DP array + O(n) recursion stack

dp[0..n][0..W] = -1
function UnboundedKnapsack(W, n):
    if n == 0 or W == 0: return 0
    if dp[n][W] != -1: return dp[n][W]
    if wt[n-1] <= W:
        dp[n][W] = max(
            val[n-1] + UnboundedKnapsack(W - wt[n-1], n),
            UnboundedKnapsack(W, n-1)
        )
    else:
        dp[n][W] = UnboundedKnapsack(W, n-1)
    return dp[n][W]

💡 Think: Memoize (i,W) with the include-same-item transition.

Approach 3: Tabulation (Bottom-Up DP)

Explanation: Iteratively fill DP table where dp[i][w] represents max value using first i items for weight w.

Time Complexity: O(n * W)

Space Complexity: O(n * W)

dp[0..n][0..W] = 0
for i = 1 to n:
    for w = 0 to W:
        if wt[i-1] <= w:
            dp[i][w] = max(val[i-1] + dp[i][w - wt[i-1]], dp[i-1][w])
        else:
            dp[i][w] = dp[i-1][w]
return dp[n][W]

💡 Think: dp[i][w] considers taking item i multiple times vs skipping it.

Approach 4: Space Optimization

Explanation: Use a 1D DP array, update dp[w] for each item to save space.

Time Complexity: O(n * W)

Space Complexity: O(W)

dp[0..W] = 0
for i = 0 to n-1:
    for w = wt[i] to W:
        dp[w] = max(dp[w], val[i] + dp[w - wt[i]])
return dp[W]

💡 Think: Iterate w increasing so dp[w] can reuse dp[w - wt[i]] for unlimited picks.

Solve on LeetCode