Longest Common Subsequence (LCS)

Problem Statement

Given two strings s1 and s2, find the length of their longest common subsequence (LCS). A subsequence is a sequence that appears in the same relative order, but not necessarily contiguous.

Example: Input: s1 = "abcde", s2 = "ace", Output: 3 ("ace")

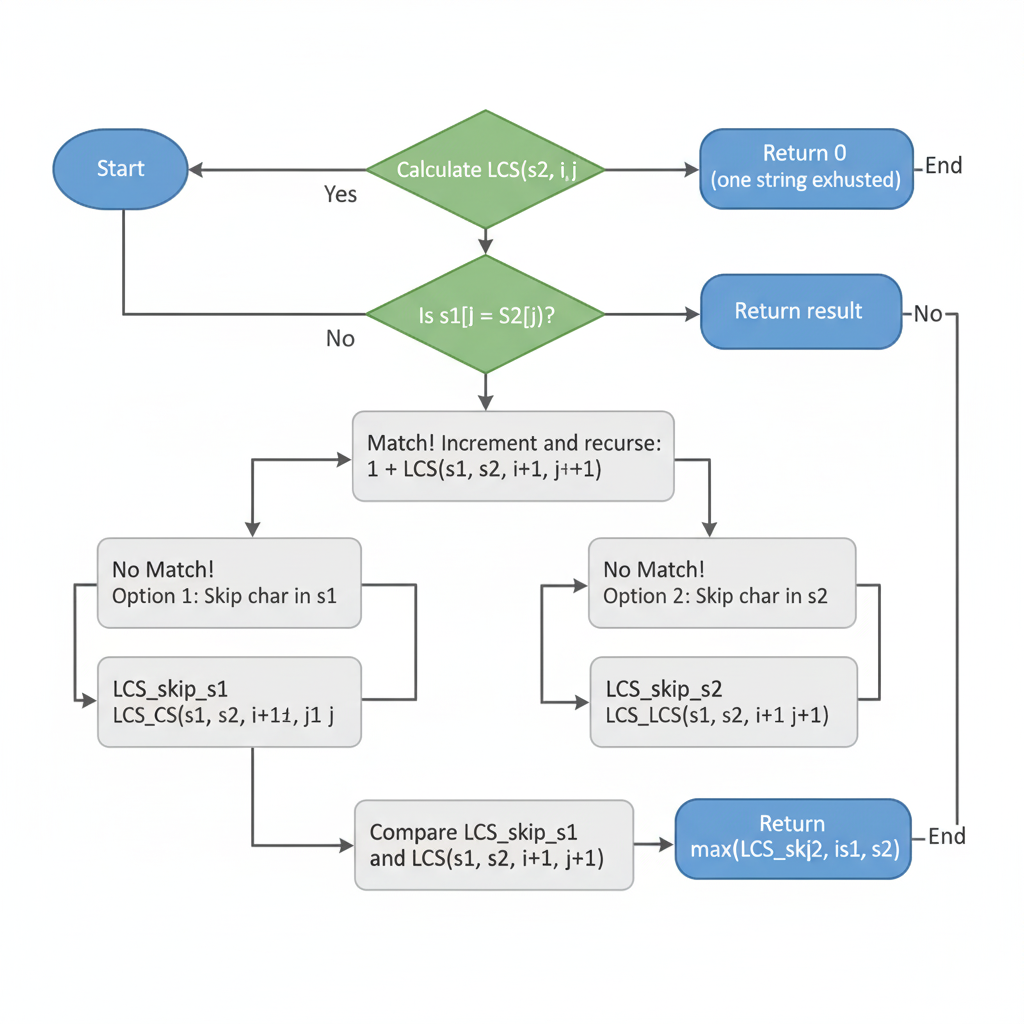
Approach 1: Recursion

Explanation: Compare characters at current indices. If match, move both pointers. Else, take max by skipping either character.

Time Complexity: O(2^m+n)

Space Complexity: O(m+n) recursion stack

function LCS(s1, s2, i, j):
    if i == len(s1) or j == len(s2): return 0
    if s1[i] == s2[j]:
        return 1 + LCS(s1, s2, i+1, j+1)
    return max(LCS(s1, s2, i+1, j), LCS(s1, s2, i, j+1))

💡 Think: Match chars to move diagonally; else take the better of skipping either side.

Approach 2: Memoization (Top-Down DP)

Explanation: Store results of subproblems (i, j) in DP array to avoid recomputation.

Time Complexity: O(m * n)

Space Complexity: O(m * n) DP array + O(m+n) recursion stack

dp[0..m][0..n] = -1
function LCS(i, j):
    if i == m or j == n: return 0
    if dp[i][j] != -1: return dp[i][j]
    if s1[i] == s2[j]:
        dp[i][j] = 1 + LCS(i+1, j+1)
    else:
        dp[i][j] = max(LCS(i+1, j), LCS(i, j+1))
    return dp[i][j]

💡 Think: Memoize (i,j) to make the exponential tree collapse to m×n.

Approach 3: Tabulation (Bottom-Up DP)

Explanation: Fill a 2D DP table iteratively from the base case.

Time Complexity: O(m * n)

Space Complexity: O(m * n)

dp[0..m][0..n] = 0
for i = m-1 to 0:
    for j = n-1 to 0:
        if s1[i] == s2[j]:
            dp[i][j] = 1 + dp[i+1][j+1]
        else:
            dp[i][j] = max(dp[i+1][j], dp[i][j+1])
return dp[0][0]

💡 Think: Fill dp bottom-up from the ends toward the start.

Approach 4: Space Optimization

Explanation: Use two 1D arrays (current and next) instead of full 2D DP table.

Time Complexity: O(m * n)

Space Complexity: O(n)

prev = [0]*(n+1)
curr = [0]*(n+1)
for i = m-1 to 0:
    for j = n-1 to 0:
        if s1[i] == s2[j]:
            curr[j] = 1 + prev[j+1]
        else:
            curr[j] = max(prev[j], curr[j+1])
    prev = curr
return prev[0]

💡 Think: Keep only two rows/columns to reduce space to O(min(m,n)).

Solve on LeetCode