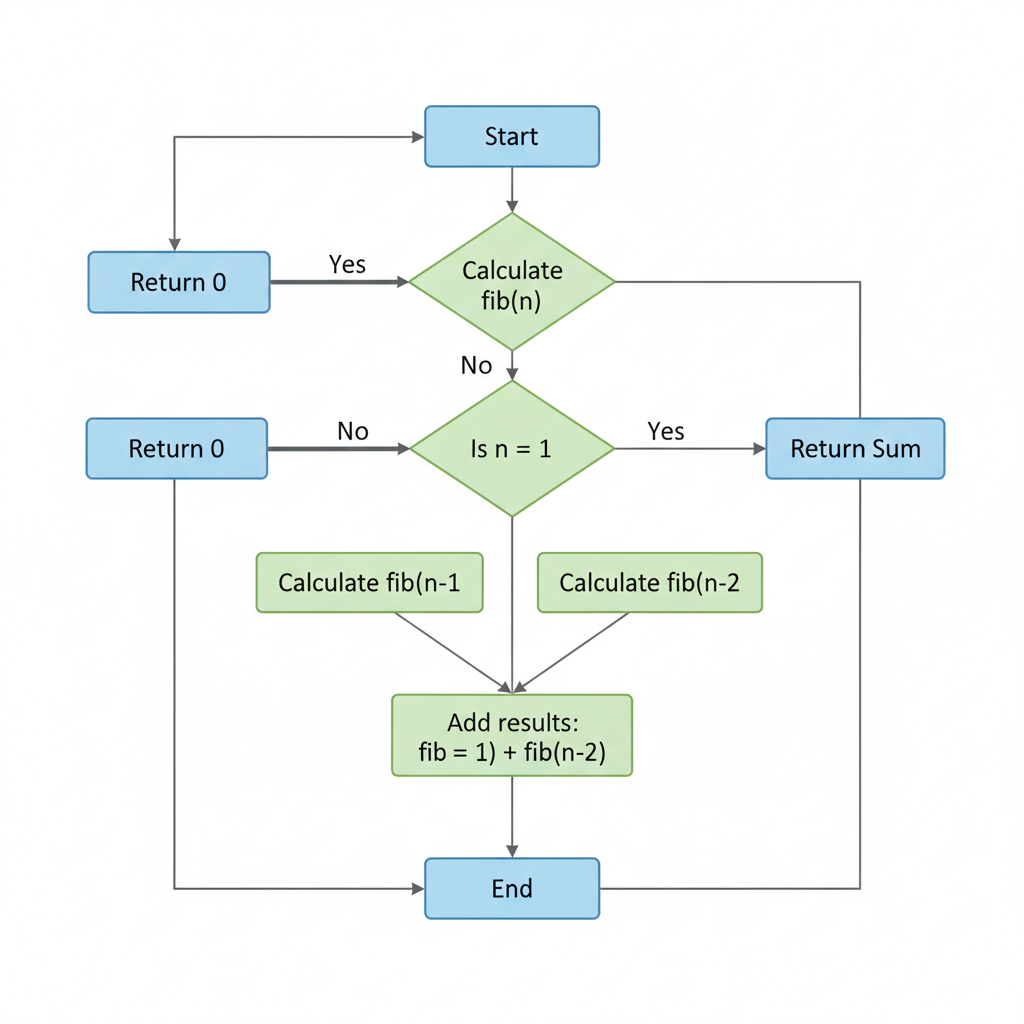
Fibonacci Sequence
Problem Statement
Given an integer n, return the nth number in the Fibonacci sequence. The sequence is defined as:
F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2) for n > 1
Example: Input: n = 6, Output: 8
Approach 1: Recursion
Explanation: Direct recursive definition of Fibonacci.
Time Complexity: O(2n)
Space Complexity: O(n) recursion stack
function fib(n):
if n == 0: return 0
if n == 1: return 1
return fib(n-1) + fib(n-2)
💡 Think: Follow the definition directly; split into two smaller subproblems each time.
Approach 2: Memoization (Top-Down DP)
Explanation: Store results of subproblems to avoid recomputation.
Time Complexity: O(n)
Space Complexity: O(n)
memo = [-1]*(n+1)
function fib(n):
if n == 0: return 0
if n == 1: return 1
if memo[n] != -1: return memo[n]
memo[n] = fib(n-1) + fib(n-2)
return memo[n]
💡 Think: Cache fib(n) results so each n is solved once, not repeatedly.
Approach 3: Tabulation (Bottom-Up DP)
Explanation: Build DP array iteratively.
Time Complexity: O(n)
Space Complexity: O(n)
dp[0] = 0
dp[1] = 1
for i = 2 to n:
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
💡 Think: Build from base cases up, filling dp[0..n] iteratively.
Approach 4: Space Optimized DP
Explanation: Only store last two values to save space.
Time Complexity: O(n)
Space Complexity: O(1)
a = 0, b = 1
for i = 2 to n:
c = a + b
a = b
b = c
return b
💡 Think: Keep only last two values and roll them forward for O(1) space.