Catalan Numbers

Problem Statement

The n-th Catalan number counts the number of valid expressions, binary search trees, or ways to parenthesize expressions. Compute the n-th Catalan number efficiently.

Example: Input: n = 4, Output: 14 (valid BSTs / valid parentheses sequences)

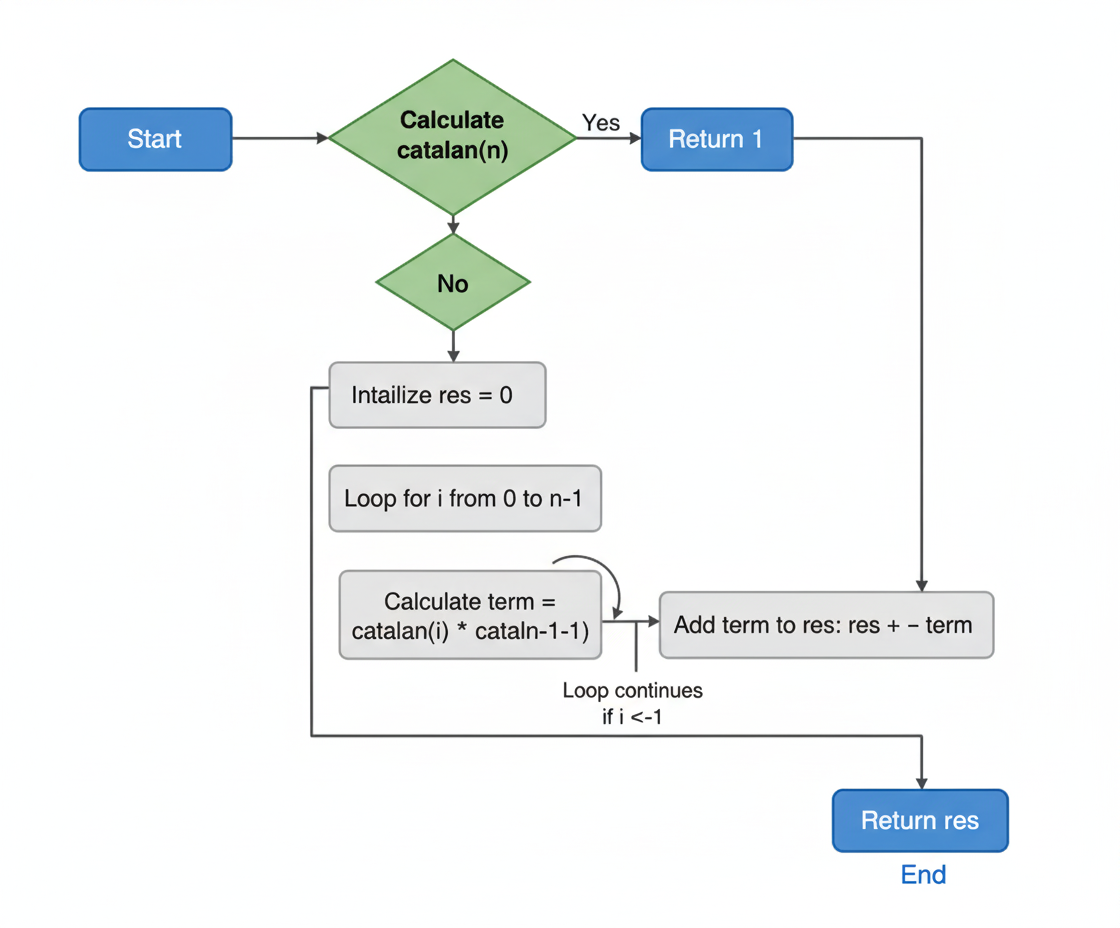
Approach 1: Recursion

Explanation: Catalan number can be defined recursively: C_n = Σ C_i * C_n-i-1 for i=0..n-1

Time Complexity: O(2ⁿ)

Space Complexity: O(n) recursion stack

function catalan(n):
    if n == 0 or n == 1: return 1
    res = 0
    for i = 0 to n-1:
        res += catalan(i) * catalan(n-i-1)
    return res

💡 Think: Sum over all splits: left subtree count × right subtree count.

Approach 2: Memoization (Top-Down DP)

Explanation: Store results of subproblems to avoid recomputation.

Time Complexity: O(n²)

Space Complexity: O(n) recursion stack + O(n) DP array

dp[0..n] = -1
function catalan(n):
    if n == 0 or n == 1: return 1
    if dp[n] != -1: return dp[n]
    res = 0
    for i = 0 to n-1:
        res += catalan(i) * catalan(n-i-1)
    dp[n] = res
    return res

💡 Think: Cache C(n) so each size is computed just once.

Approach 3: Tabulation (Bottom-Up DP)

Explanation: Compute all Catalan numbers from 0 to n iteratively.

Time Complexity: O(n²)

Space Complexity: O(n)

dp[0] = dp[1] = 1
for k = 2 to n:
    dp[k] = 0
    for i = 0 to k-1:
        dp[k] += dp[i] * dp[k-i-1]
return dp[n]

💡 Think: Compute C(0..n) iteratively via the convolution formula.

Approach 4: Using Binomial Coefficient

Explanation: Catalan(n) = C(2n, n) / (n+1)

Time Complexity: O(n)

Space Complexity: O(1)

function catalan(n):
    return binomialCoefficient(2*n, n) / (n + 1)

💡 Think: Use C(2n,n)/(n+1) for a direct, efficient computation.

Solve on LeetCode