Tree Traversals
Problem Statement
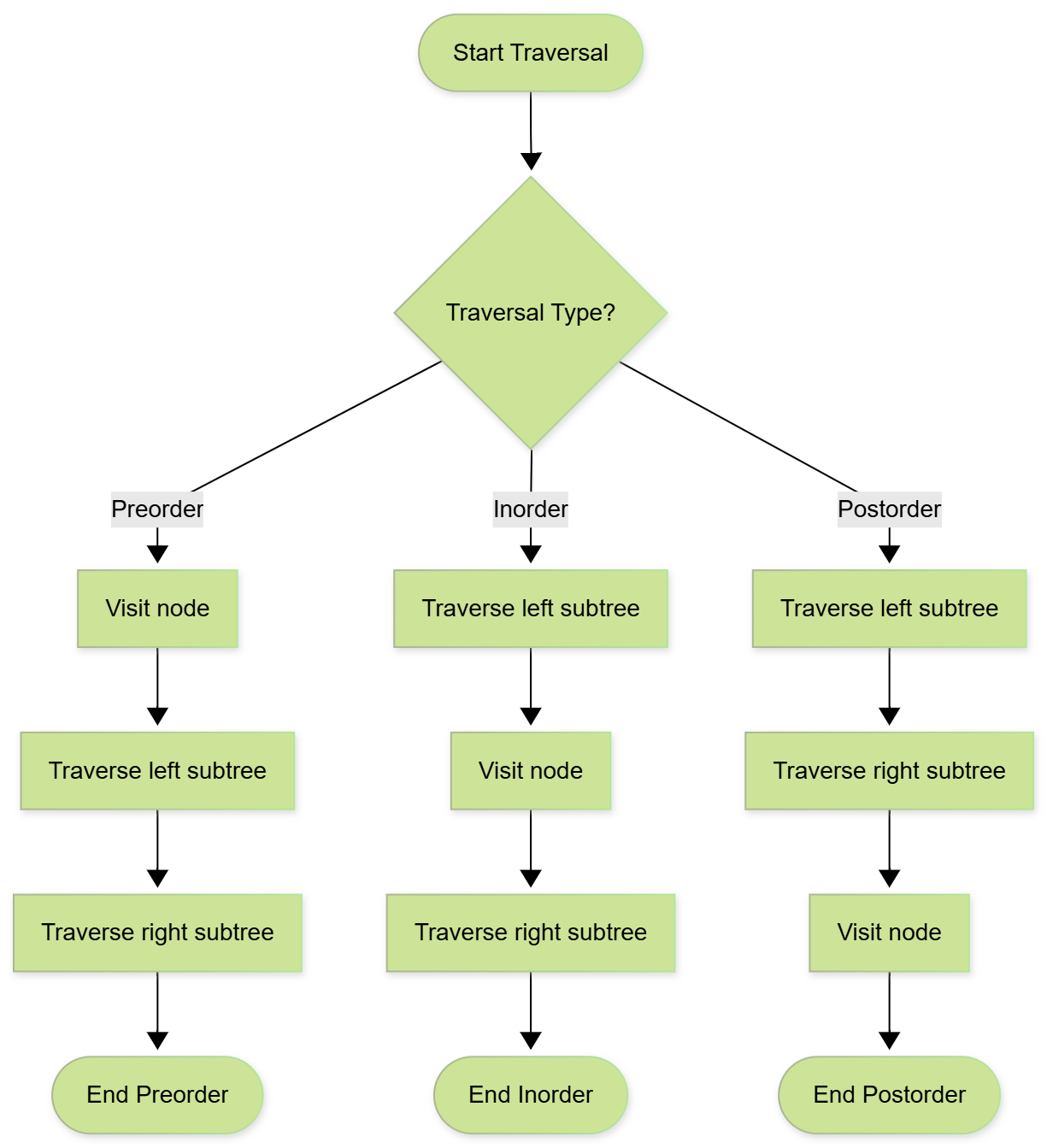
Given the root of a binary tree, traverse it in different orders: inorder, preorder, and postorder.
Example:
1
/ \
2 3
/ \
4 5
Inorder → [4,2,5,1,3]
Preorder → [1,2,4,5,3]
Postorder → [4,5,2,3,1]
Approach 1: Recursive Traversal
Explanation: Use standard recursion for inorder, preorder, and postorder.
Time Complexity: O(n)
Space Complexity: O(h) for recursion stack, where h is tree height
// Inorder
inorder(node):
if node == NULL: return
inorder(node.left)
print(node.val)
inorder(node.right)
// Preorder
preorder(node):
if node == NULL: return
print(node.val)
preorder(node.left)
preorder(node.right)
// Postorder
postorder(node):
if node == NULL: return
postorder(node.left)
postorder(node.right)
print(node.val)
💡 Think: Visit left, node, right (or node first, or node last) using call stack to control order.
Approach 2: Iterative Using Stack
Explanation: Use a stack to simulate recursion for inorder, preorder, or postorder traversal.
Time Complexity: O(n)
Space Complexity: O(h)
// Iterative Inorder
stack = empty
curr = root
while curr != NULL or stack not empty:
while curr != NULL:
stack.push(curr)
curr = curr.left
curr = stack.pop()
print(curr.val)
curr = curr.right
💡 Think: Simulate recursion with a stack to push lefts, pop node, then go right.
Approach 3: Morris Traversal (Inorder, O(1) space)
Explanation: Threaded binary tree technique to traverse without recursion or stack.
Time Complexity: O(n)
Space Complexity: O(1)
curr = root
while curr != NULL:
if curr.left == NULL:
print(curr.val)
curr = curr.right
else:
predecessor = curr.left
while predecessor.right != NULL and predecessor.right != curr:
predecessor = predecessor.right
if predecessor.right == NULL:
predecessor.right = curr
curr = curr.left
else:
predecessor.right = NULL
print(curr.val)
curr = curr.right
💡 Think: Thread predecessors temporarily to traverse in O(1) space without stack or recursion.