Lowest Common Ancestor of Binary Tree

Problem Statement

Given a binary tree and two nodes p and q, find their lowest common ancestor (LCA). The LCA is the lowest node in the tree that has both p and q as descendants (a node can be a descendant of itself).

Example:

        3
       / \
      5   1
     / \ / \
    6  2 0  8
      / \
     7   4

LCA(5,1) = 3
LCA(6,4) = 5

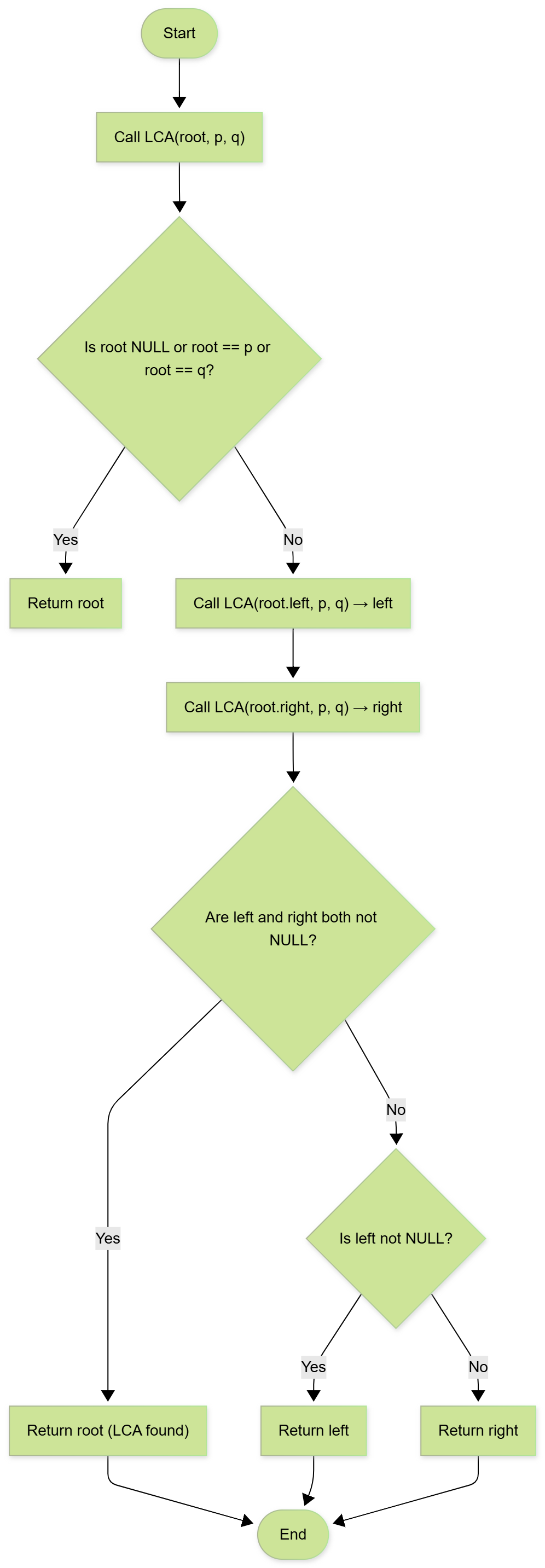
Approach 1: Recursive DFS

Explanation: Traverse tree recursively. If node is p or q, return it. Combine left and right results to find LCA.

Time Complexity: O(n)

Space Complexity: O(h) recursion stack

function LCA(root, p, q):
    if root == NULL or root == p or root == q: return root
    left = LCA(root.left, p, q)
    right = LCA(root.right, p, q)
    if left != NULL and right != NULL: return root
    return left if left != NULL else right

💡 Think: Return node when found; if both sides return non-null, current is LCA.

Approach 2: Parent Pointers + Ancestor Set

Explanation: Store parent of each node in a hash map. Trace ancestors of p, then first ancestor of q in the set is LCA.

Time Complexity: O(n)

Space Complexity: O(n)

parent = {root: NULL}
stack = [root]
while stack not empty:
    node = stack.pop()
    if node.left:
        parent[node.left] = node
        stack.push(node.left)
    if node.right:
        parent[node.right] = node
        stack.push(node.right)

ancestors = set()
while p != NULL:
    ancestors.add(p)
    p = parent[p]
while q not in ancestors:
    q = parent[q]
return q

💡 Think: Record ancestors of p; climb q until you hit the set.

Approach 3: Iterative DFS

Explanation: Use stack for DFS and store path to p and q. Compare paths to find last common node.

Time Complexity: O(n)

Space Complexity: O(n)

function findPath(root, target):
    stack = [(root,[root])]
    while stack:
        node, path = stack.pop()
        if node == target: return path
        if node.right: stack.push((node.right,path+[node.right]))
        if node.left: stack.push((node.left,path+[node.left]))
        
pathP = findPath(root,p)
pathQ = findPath(root,q)
LCA = NULL
for i in 0..min(len(pathP),len(pathQ))-1:
    if pathP[i] == pathQ[i]:
        LCA = pathP[i]
    else:
        break
return LCA

💡 Think: Build root→p and root→q paths; last common node is the LCA.

Solve on LeetCode