Height & Diameter of Binary Tree

Problem Statement

Given the root of a binary tree, calculate:
1. Height: The number of nodes along the longest path from root to leaf.
2. Diameter: The length of the longest path between any two nodes.

Example:

       1
      / \
     2   3
    / \
   4   5

Height = 3
Diameter = 4 (path: 4 → 2 → 1 → 3)

Approach 1: Height and Diameter Separately

Explanation: Compute height recursively for each node and calculate diameter as leftHeight + rightHeight + 1.

Time Complexity: O(n²) in worst case (recomputing heights)

Space Complexity: O(h) recursion stack

function height(node):
    if node == NULL: return 0
    return 1 + max(height(node.left), height(node.right))

function diameter(node):
    if node == NULL: return 0
    leftHeight = height(node.left)
    rightHeight = height(node.right)
    leftDia = diameter(node.left)
    rightDia = diameter(node.right)
    return max(leftHeight + rightHeight + 1, max(leftDia, rightDia))

💡 Think: Recompute heights per node; diameter is leftH + rightH (+1 if counting nodes).

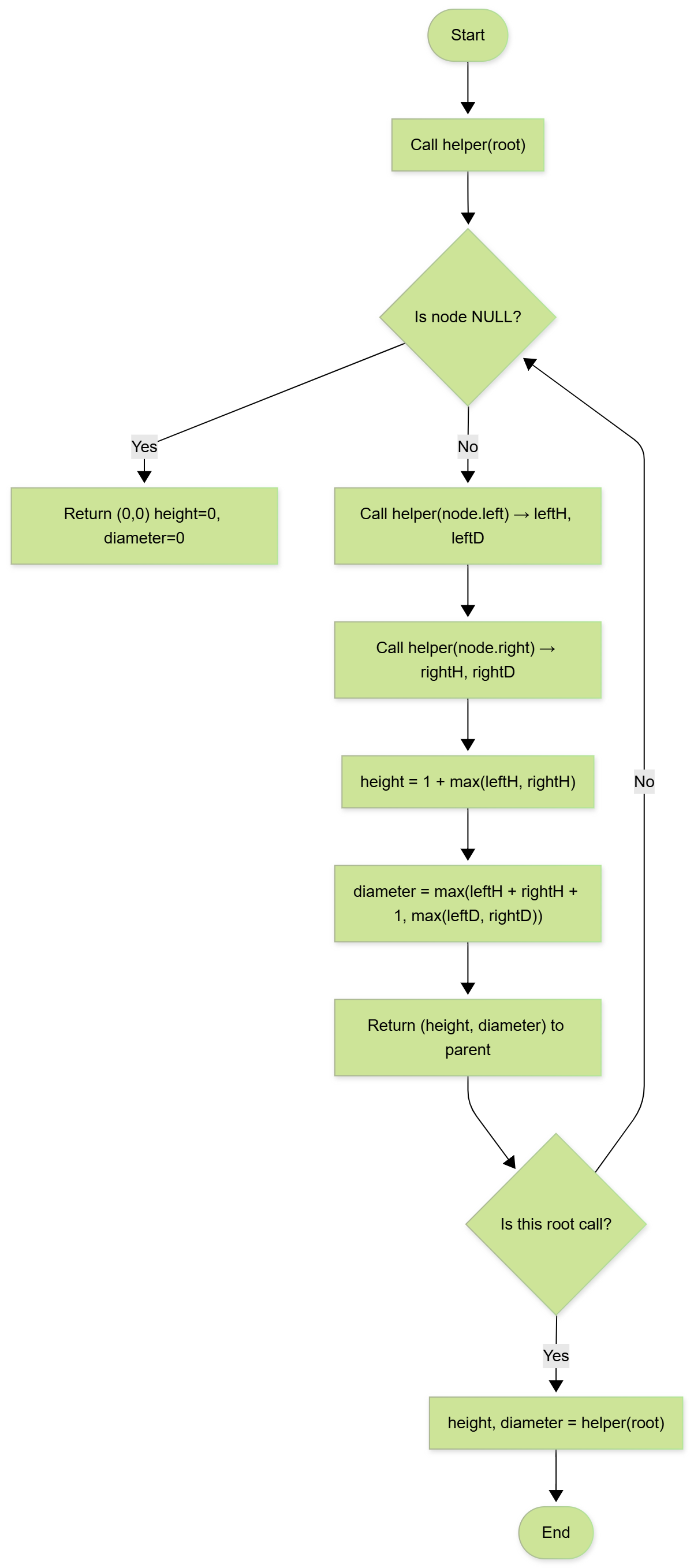
Approach 2: Single Pass (Optimized)

Explanation: Return height along with diameter from a recursive function to avoid recomputation.

Time Complexity: O(n)

Space Complexity: O(h)

function helper(node):
    if node == NULL: return (0,0)  // (height, diameter)
    leftH, leftD = helper(node.left)
    rightH, rightD = helper(node.right)
    height = 1 + max(leftH, rightH)
    diameter = max(leftH + rightH + 1, max(leftD, rightD))
    return (height, diameter)

height, diameter = helper(root)

💡 Think: Return (height, diameter) together so each node is processed once.

Approach 3: Iterative Using Postorder

Explanation: Use stack to traverse in postorder, storing height at each node to compute diameter iteratively.

Time Complexity: O(n)

Space Complexity: O(h)

stack = empty
mapHeight = {}
push root to stack
while stack not empty:
    node = stack.top()
    if node.left and node.left not in mapHeight:
        push node.left
        continue
    if node.right and node.right not in mapHeight:
        push node.right
        continue
    pop node
    leftH = mapHeight.get(node.left,0)
    rightH = mapHeight.get(node.right,0)
    mapHeight[node] = 1 + max(leftH, rightH)
    diameter = max(diameter, leftH + rightH + 1)

💡 Think: Postorder with stored heights; update best diameter at each pop.

Solve on LeetCode