Maximum Path Sum

Problem Statement

Given a non-empty binary tree, find the maximum path sum. A path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Example:

Input:       1
            / \
           2   3
Output: 6 (2 → 1 → 3)

Approach 1: Recursive DFS with Global Max

Explanation: At each node, compute max path sum including left/right children. Update global maximum including both sides.

Time Complexity: O(n)

Space Complexity: O(h) (recursion stack, h = tree height)

maxSum = -∞
function maxPathSum(node):
    if node == NULL: return 0
    left = max(0, maxPathSum(node.left))
    right = max(0, maxPathSum(node.right))
    maxSum = max(maxSum, node.val + left + right)
    return node.val + max(left, right)

return maxSum

💡 Think: At each node take max(0,left), max(0,right); update global with node+left+right.

Approach 2: Iterative Postorder DFS

Explanation: Use a stack for postorder traversal. Track max path sum at each node using a hashmap to store results of left/right children.

Time Complexity: O(n)

Space Complexity: O(n) (stack + hashmap)

stack = [(root, False)]
maxMap = {}
maxSum = -∞
while stack:
    node, visited = stack.pop()
    if node is NULL: continue
    if visited:
        left = max(0, maxMap.get(node.left,0))
        right = max(0, maxMap.get(node.right,0))
        maxSum = max(maxSum, node.val + left + right)
        maxMap[node] = node.val + max(left, right)
    else:
        stack.push((node, True))
        stack.push((node.right, False))
        stack.push((node.left, False))
return maxSum

💡 Think: Compute child gains via stack map; update global when visiting node.

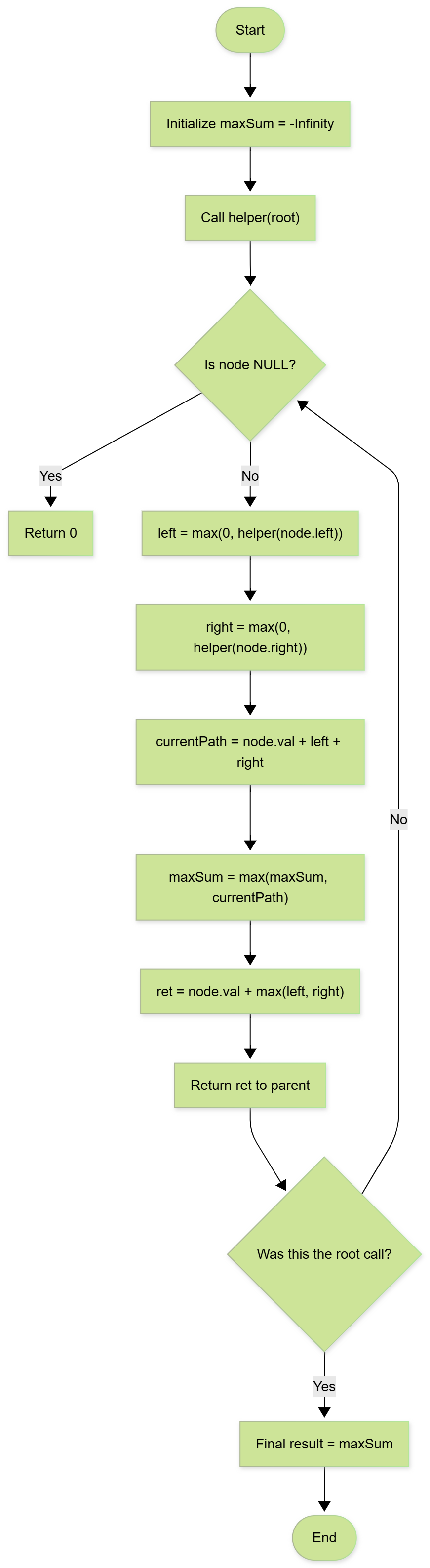
Approach 3: DFS with Return Values Only

Explanation: Recursive DFS returns max sum for parent-child path. Global variable tracks overall max including both children.

Time Complexity: O(n)

Space Complexity: O(h)

maxSum = -∞
function helper(node):
    if node == NULL: return 0
    left = max(0, helper(node.left))
    right = max(0, helper(node.right))
    maxSum = max(maxSum, node.val + left + right)
    return node.val + max(left, right)

helper(root)
return maxSum

💡 Think: Return single-branch gain upward; track best split-path in a global.

Solve on LeetCode