Insert & Search in BST

LeetCode #701 [Medium]

Problem Statement

Implement insert and search operations in a Binary Search Tree (BST).

Example: Insert 5, 3, 7, 2, 4 → Search 4 → Output: Found

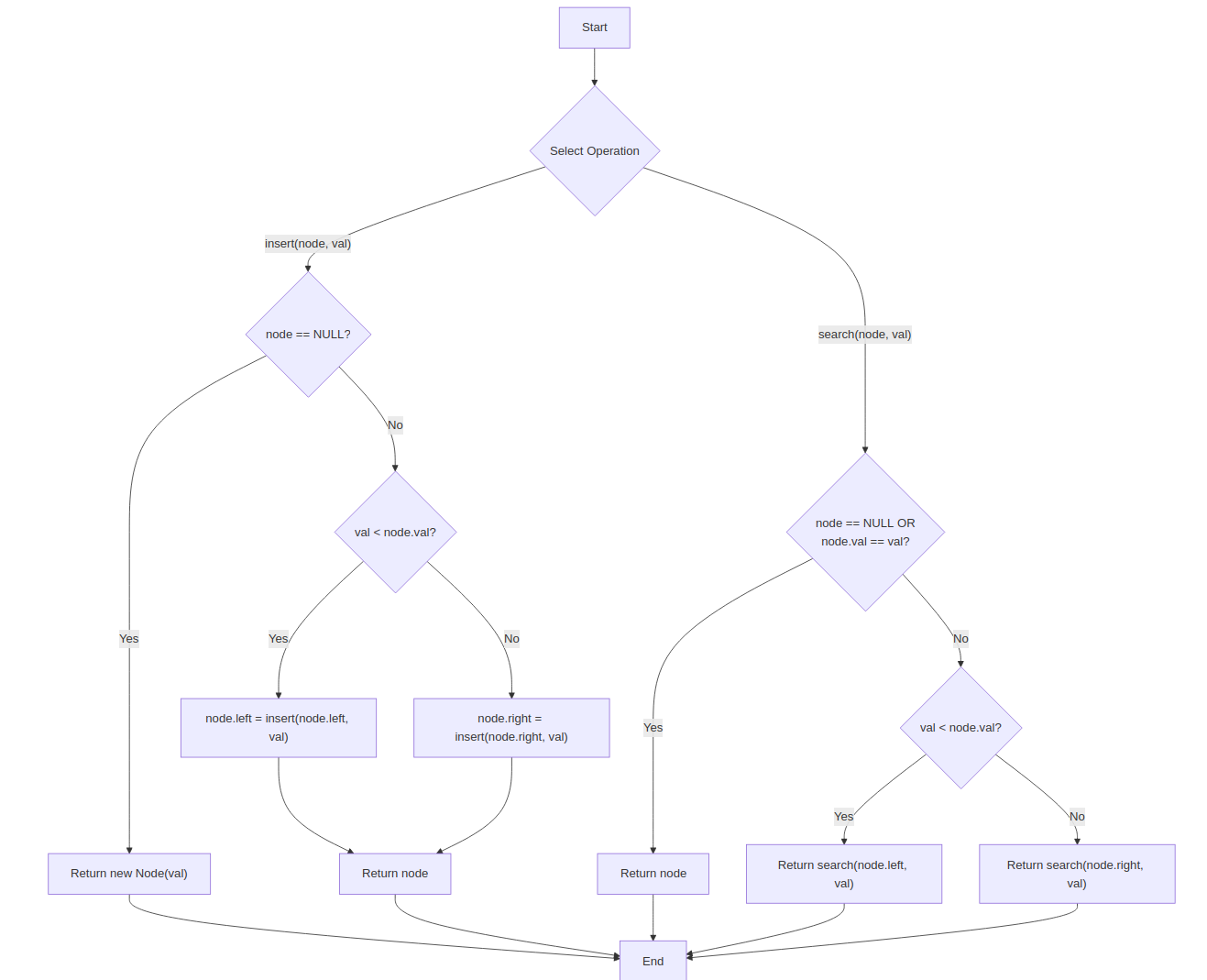
Approach 1: Recursive Insertion & Search

Explanation: Insert by comparing with root and recur left/right. Search similarly.

Time Complexity: O(h), where h is height of BST

Space Complexity: O(h) due to recursion stack

function insert(node, val):
    if node == NULL:
        return new Node(val)
    if val < node.val:
        node.left = insert(node.left, val)
    else:
        node.right = insert(node.right, val)
    return node

function search(node, val):
    if node == NULL or node.val == val:
        return node
    if val < node.val:
        return search(node.left, val)
    return search(node.right, val)
Heap Sort Flowchart

💡 Think: Compare with node and branch left/right until you place/find the value.

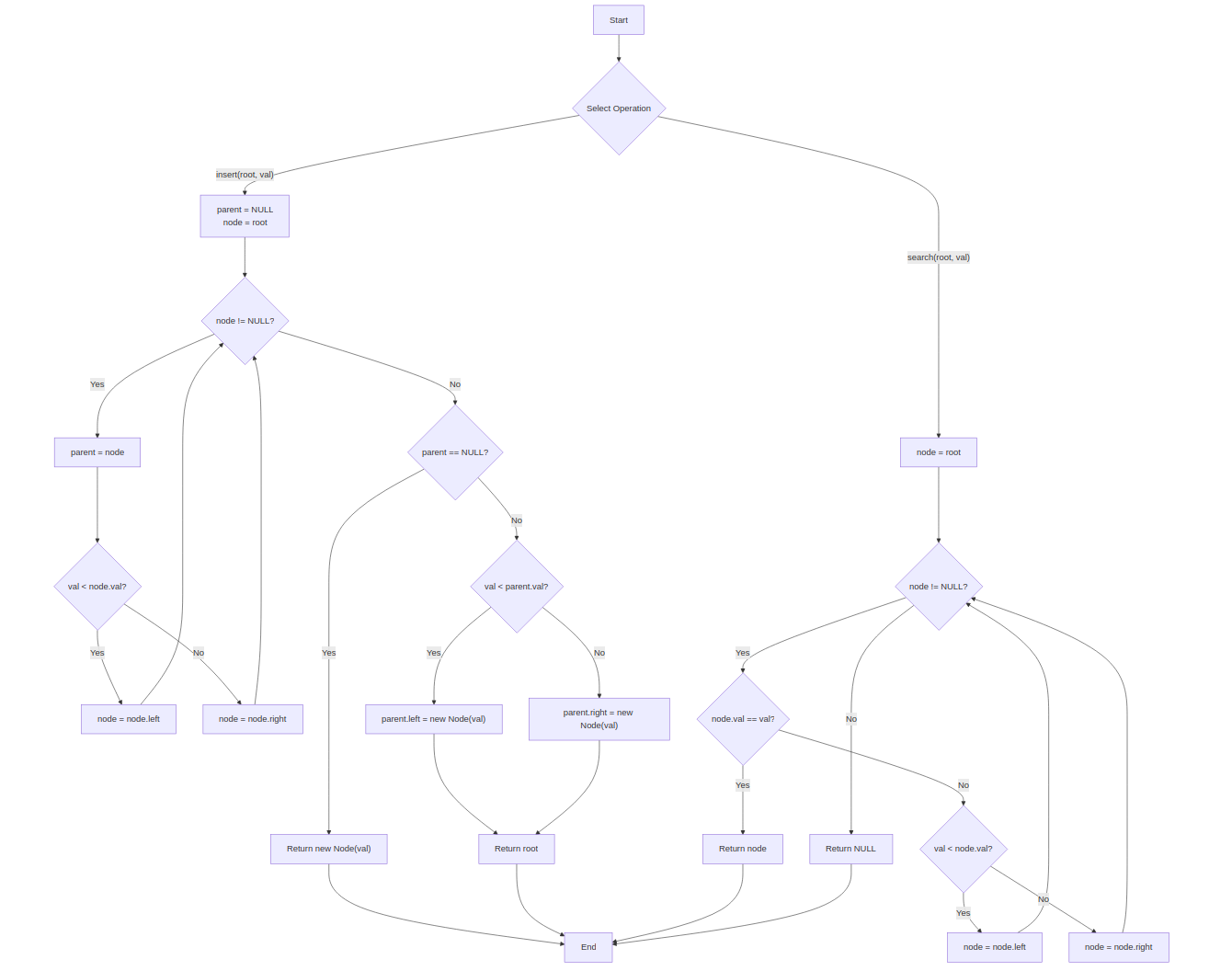
Approach 2: Iterative Insertion & Search

Explanation: Traverse iteratively to insert or search without recursion.

Time Complexity: O(h)

Space Complexity: O(1)

function insert(root, val):
    parent = NULL
    node = root
    while node != NULL:
        parent = node
        if val < node.val:
            node = node.left
        else:
            node = node.right
    if parent == NULL:
        return new Node(val)
    if val < parent.val:
        parent.left = new Node(val)
    else:
        parent.right = new Node(val)
    return root

function search(root, val):
    node = root
    while node != NULL:
        if node.val == val:
            return node
        node = node.left if val < node.val else node.right
    return NULL
Heap Sort Flowchart

💡 Think: Walk down with a pointer; track parent to attach new nodes without recursion.

Solve on LeetCode