Two Sum

Problem Statement

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target. You may assume that each input would have exactly one solution, and you may not use the same element twice.

Example: nums = [2,7,11,15], target = 9 ā†’ Output: [0,1]

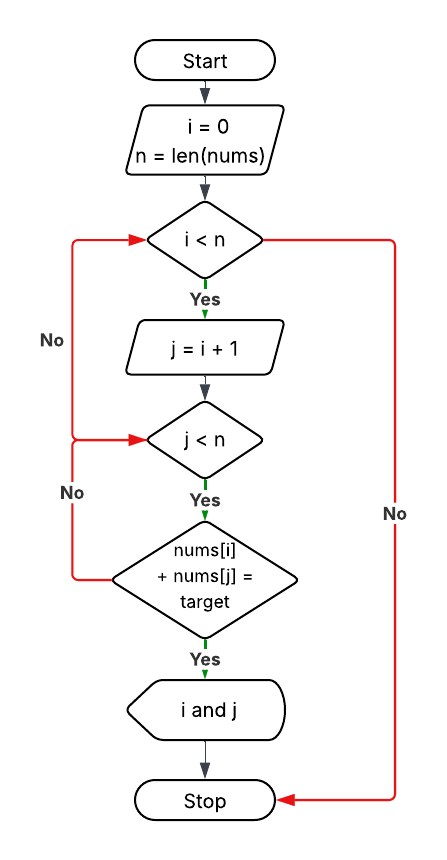
Approach 1: Brute Force

Explanation: Check all pairs of numbers to see if they sum to target.

Time Complexity: O(nĀ²)

Space Complexity: O(1)

for i = 0 to n-1:
    for j = i+1 to n-1:
        if nums[i] + nums[j] == target:
            return [i, j]

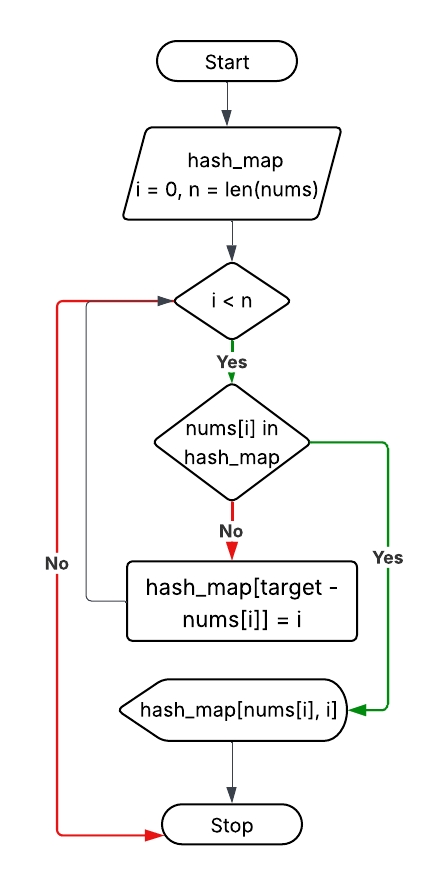
Approach 2: Using Hash Map (Better)

Explanation: Store each number's complement (target - num) in a hash map. Check if current number exists in map.

Time Complexity: O(n)

Space Complexity: O(n)

create empty hash map
for i = 0 to n-1:
    if nums[i] in map:
        return [map[nums[i]], i]
    else:
        map[target - nums[i]] = i

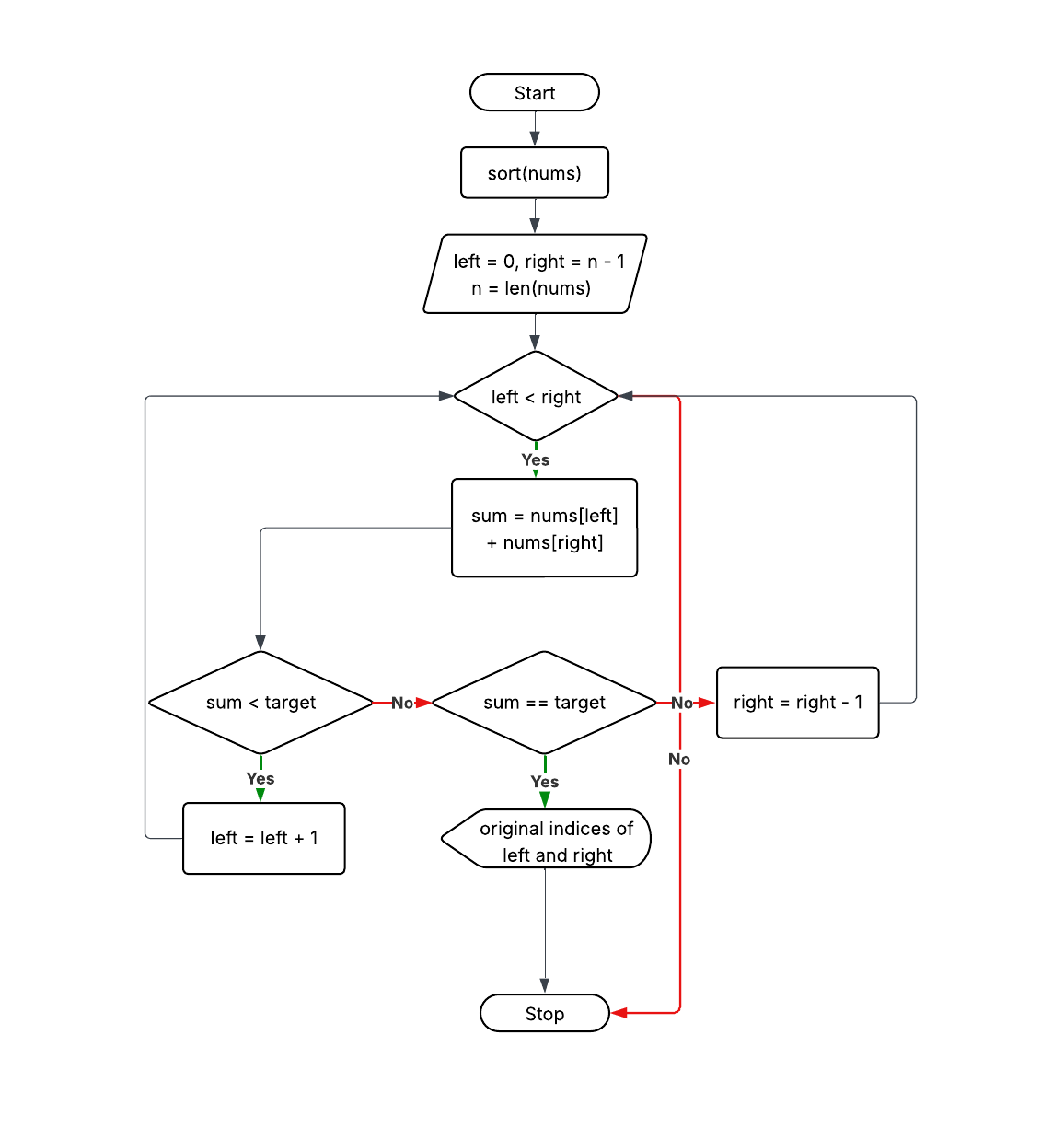
Approach 3: Two Pointers (Optimal if array sorted)

Explanation: Sort the array, use two pointers (start and end) to find sum. Return indices from original array.

Time Complexity: O(n log n) (sorting) + O(n) two pointers ā†’ O(n log n)

Space Complexity: O(n) (for storing original indices) 

sort the array with original indices
left = 0, right = n-1
while left < right:
    sum = nums[left] + nums[right]
    if sum == target:
        return original indices of nums[left] and nums[right]
    else if sum < target:
        left++
    else:
        right--