Trapping Rain Water

Problem Statement

Given an array of heights, compute how much water can be trapped after raining.

Example: heights = [0,1,0,2,1,0,1,3,2,1,2,1] → Output: 6

Approach 1: Brute Force

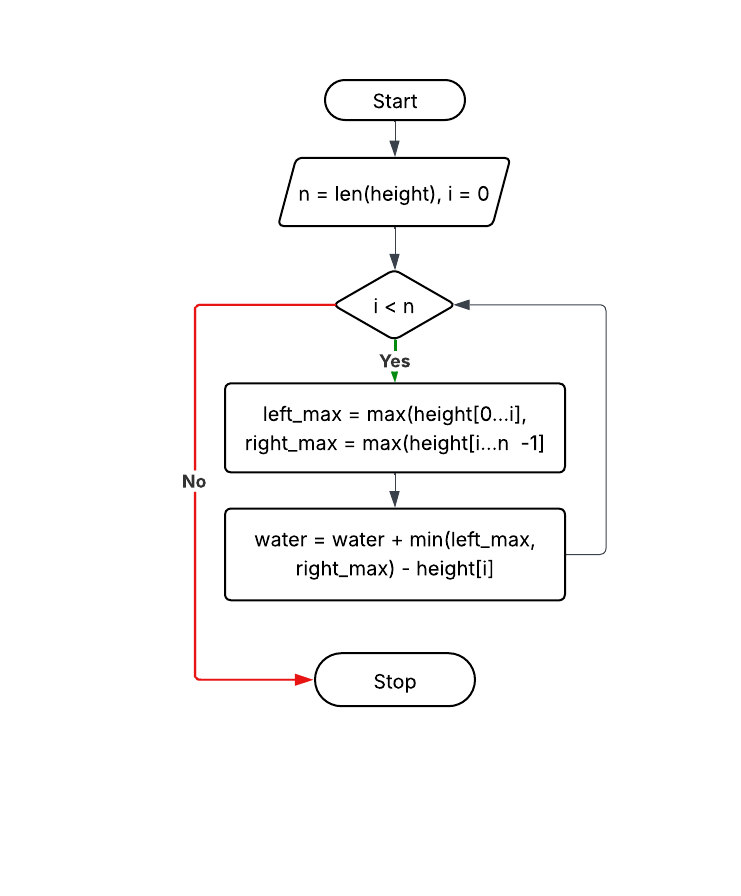
Explanation: For each element, find max left and right heights. Water trapped = min(left_max, right_max) - height[i]

Time: O(n²), Space: O(1)

for i = 0 to n-1:
  left_max = max(height[0..i])
  right_max = max(height[i..n-1])
  water += min(left_max, right_max) - height[i]

💡 Think: For each bar, what's the tallest wall on both sides to find possible trapped water?

Approach 2: Prefix & Suffix Arrays

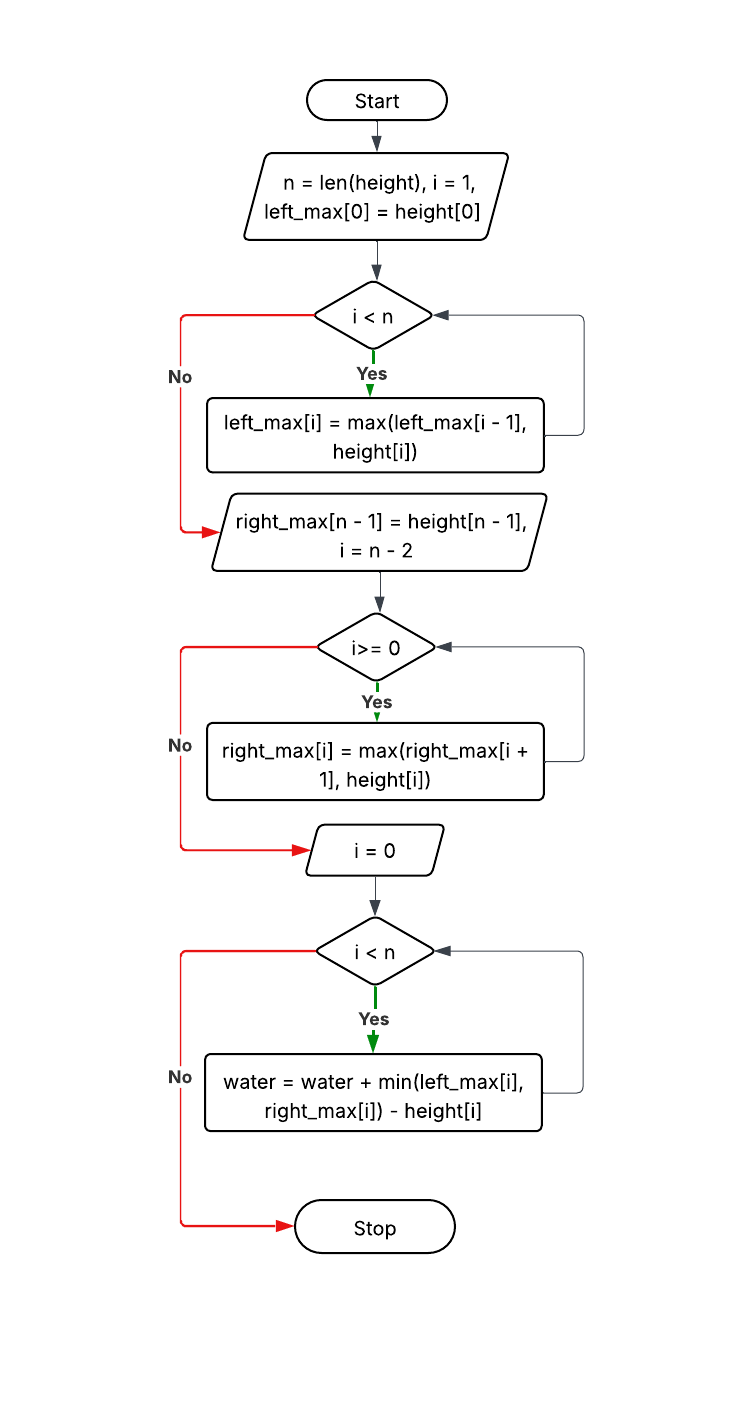
Explanation: Precompute left_max and right_max arrays to reduce repeated computation.

Time: O(n), Space: O(n)

left_max[0] = height[0]
for i = 1 to n-1: left_max[i] = max(left_max[i-1], height[i])
right_max[n-1] = height[n-1]
for i = n-2 downto 0: right_max[i] = max(right_max[i+1], height[i])
for i = 0 to n-1: water += min(left_max[i], right_max[i]) - height[i]

💡 Think: Can I store highest walls on both sides to calculate trapped water quickly?

Approach 3: Two Pointers (Optimal)

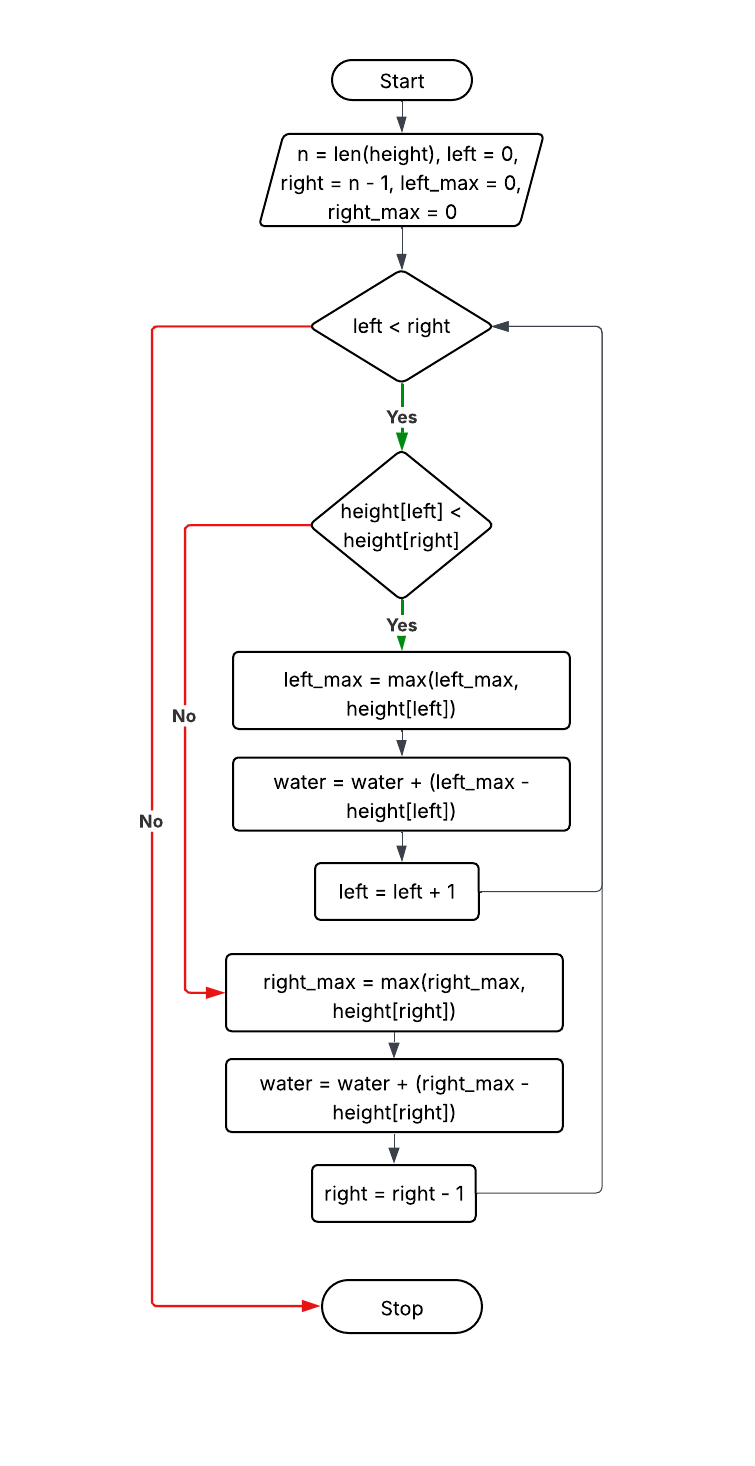
Explanation: Use two pointers, track left_max and right_max on the fly, calculate trapped water in one pass.

Time: O(n), Space: O(1)

left = 0, right = n-1
left_max = right_max = 0
while left < right:
  if height[left] < height[right]:
    left_max = max(left_max, height[left])
    water += left_max - height[left]
    left++
  else:
    right_max = max(right_max, height[right])
    water += right_max - height[right]
    right--

💡 Think: What if I track left and right max heights dynamically using two pointers in one scan?

Solve on LeetCode