Maximum Subarray

LeetCode #53 [Medium]

Problem Statement

Find the contiguous subarray with the largest sum in a given integer array.

Example: nums = [-2,1,-3,4,-1,2,1,-5,4] → Output: 6 ([4,-1,2,1])

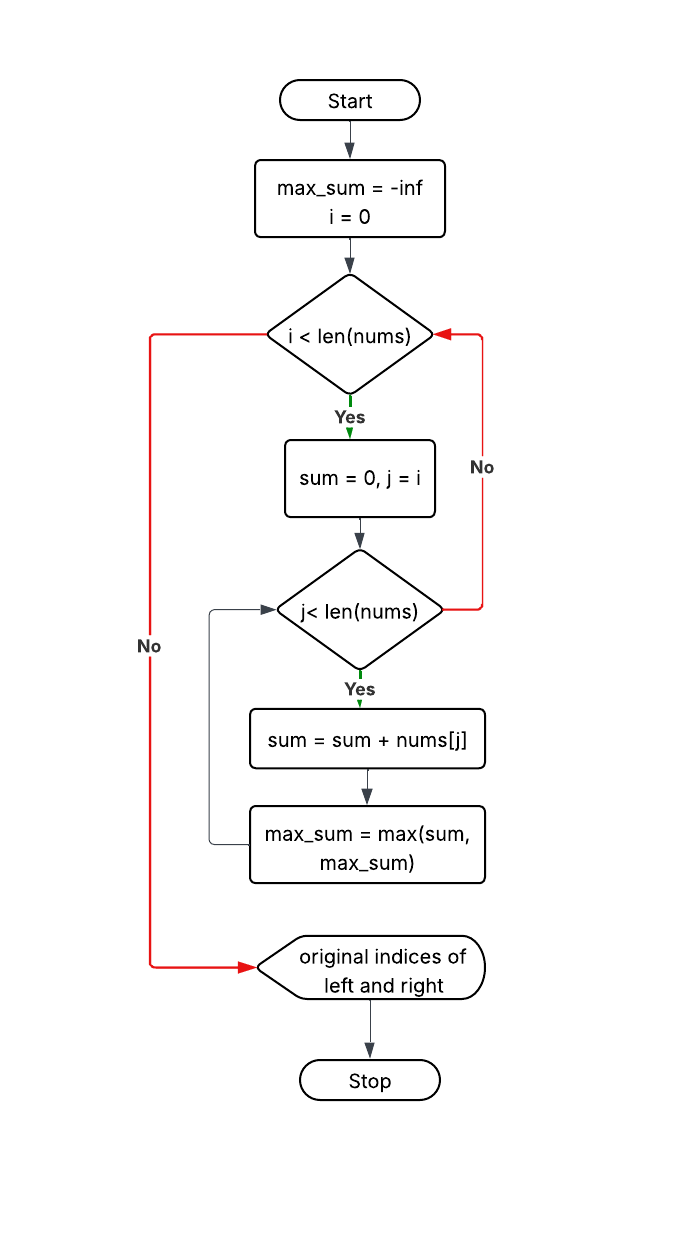
Approach 1: Brute Force

Explanation: Consider all subarrays and calculate sum.

Time Complexity: O(n²)

Space Complexity: O(1)

max_sum = -∞
for i in 0..n-1:
    sum=0
    for j in i..n-1:
        sum += nums[j]
        max_sum = max(max_sum,sum)
return max_sum
Brute force

💡 Think: What if I check every possible subarray and see which one gives the biggest sum?

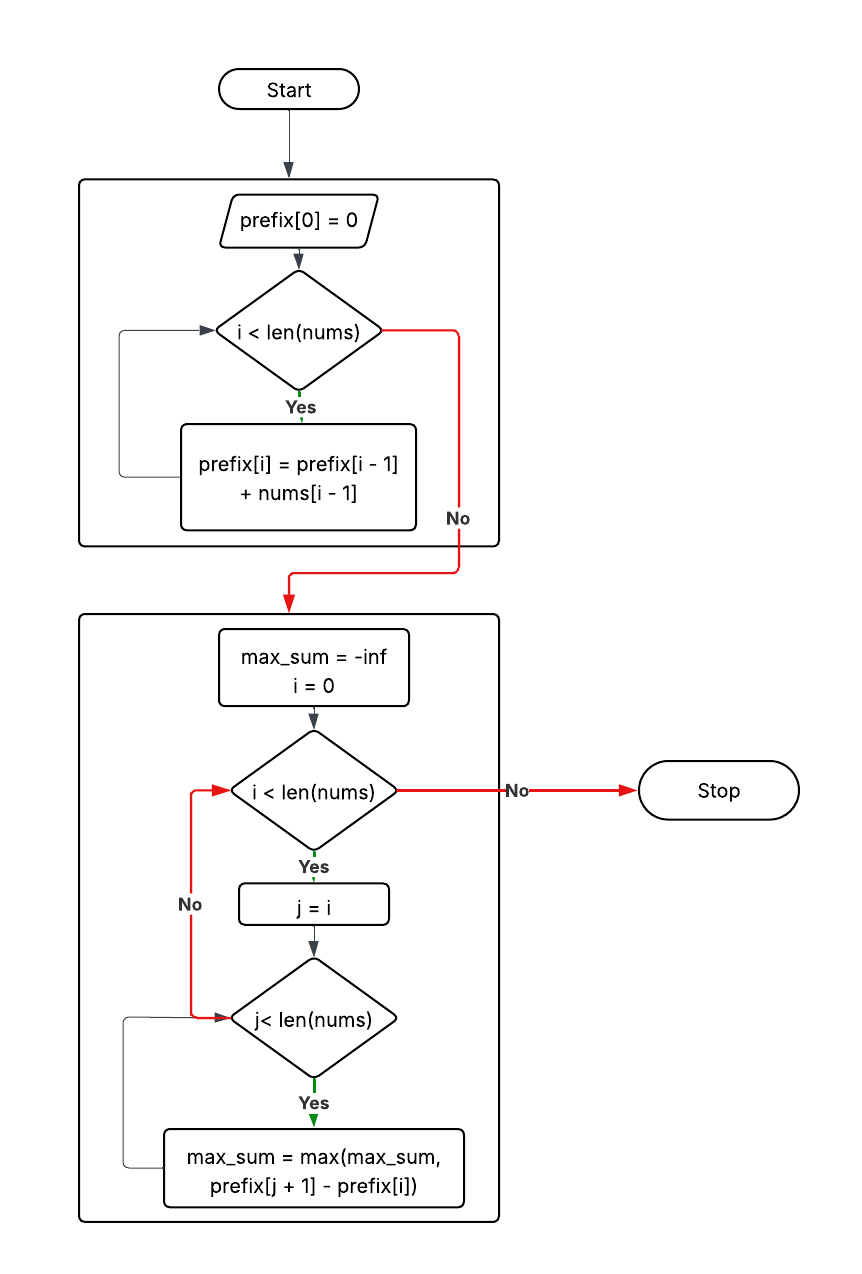
Approach 2: Prefix Sum

Explanation: Use prefix sums to compute subarray sums efficiently.

Time Complexity: O(n²)

Space Complexity: O(n)

prefix[0]=0
for i in 1..n:
    prefix[i]=prefix[i-1]+nums[i-1]
max_sum=-∞
for i in 0..n-1:
    for j in i..n-1:
        max_sum = max(max_sum, prefix[j+1]-prefix[i])
Prefix sum

💡 Think: Can I precompute running totals so I can find any subarray sum quickly without recounting?

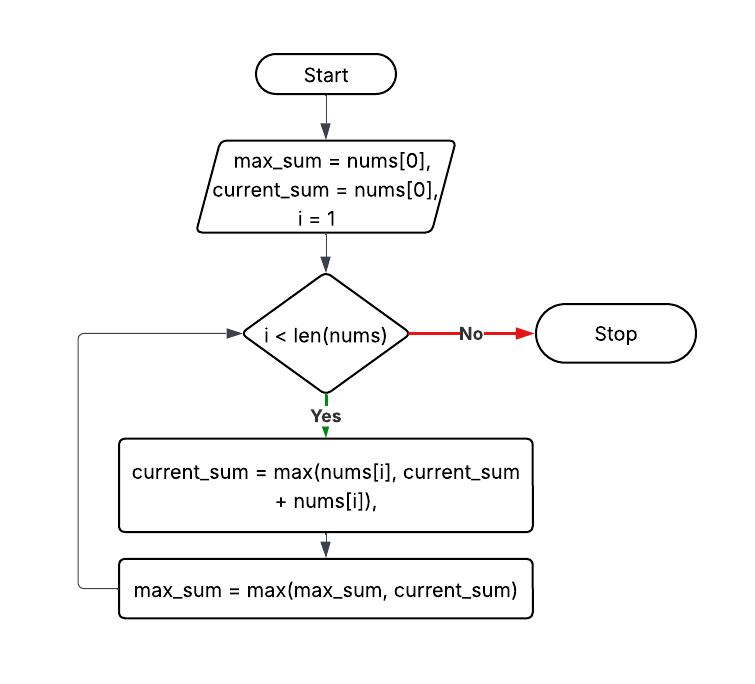
Approach 3: Kadane’s Algorithm (Optimal)

Explanation: Keep running sum; reset if sum < 0.

Time Complexity: O(n)

Space Complexity: O(1)

max_sum=nums[0]
current_sum=nums[0]
for i in 1..n-1:
    current_sum = max(nums[i], current_sum+nums[i])
    max_sum = max(max_sum, current_sum)
return max_sum
Kadane's algorithm

💡 Think: What if I keep a running total and reset it whenever it becomes negative to track the best subarray on the go?

Solve on LeetCode