Container With Most Water

Problem Statement

Given an array of heights, find two lines that together with x-axis form a container holding the most water.

Example: heights = [1,8,6,2,5,4,8,3,7] → Output: 49

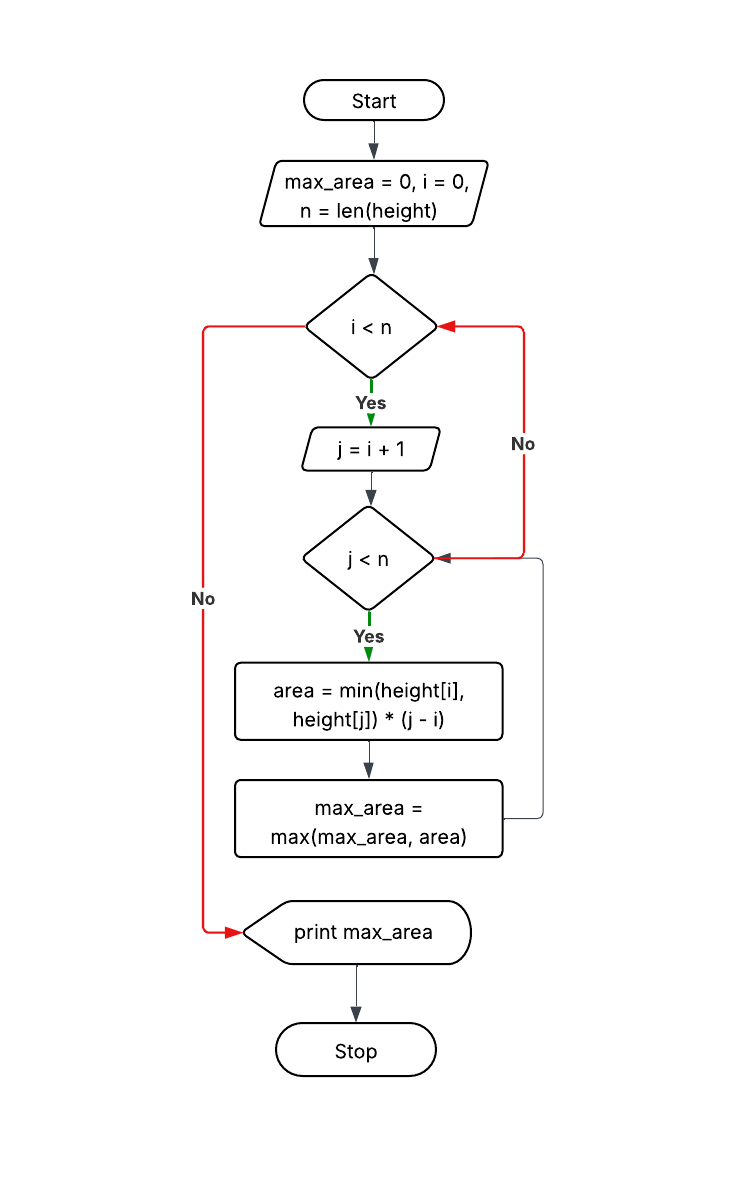
Approach 1: Brute Force

Explanation: Check every pair of lines and calculate area.

Time: O(n²), Space: O(1)

        max_area = 0
        for i = 0 to n-1:
        for j = i+1 to n-1:
        area = min(height[i], height[j]) * (j - i)
        max_area = max(max_area, area)
        return max_area

💡 Think: What if I try every pair of lines and calculate all possible container areas?

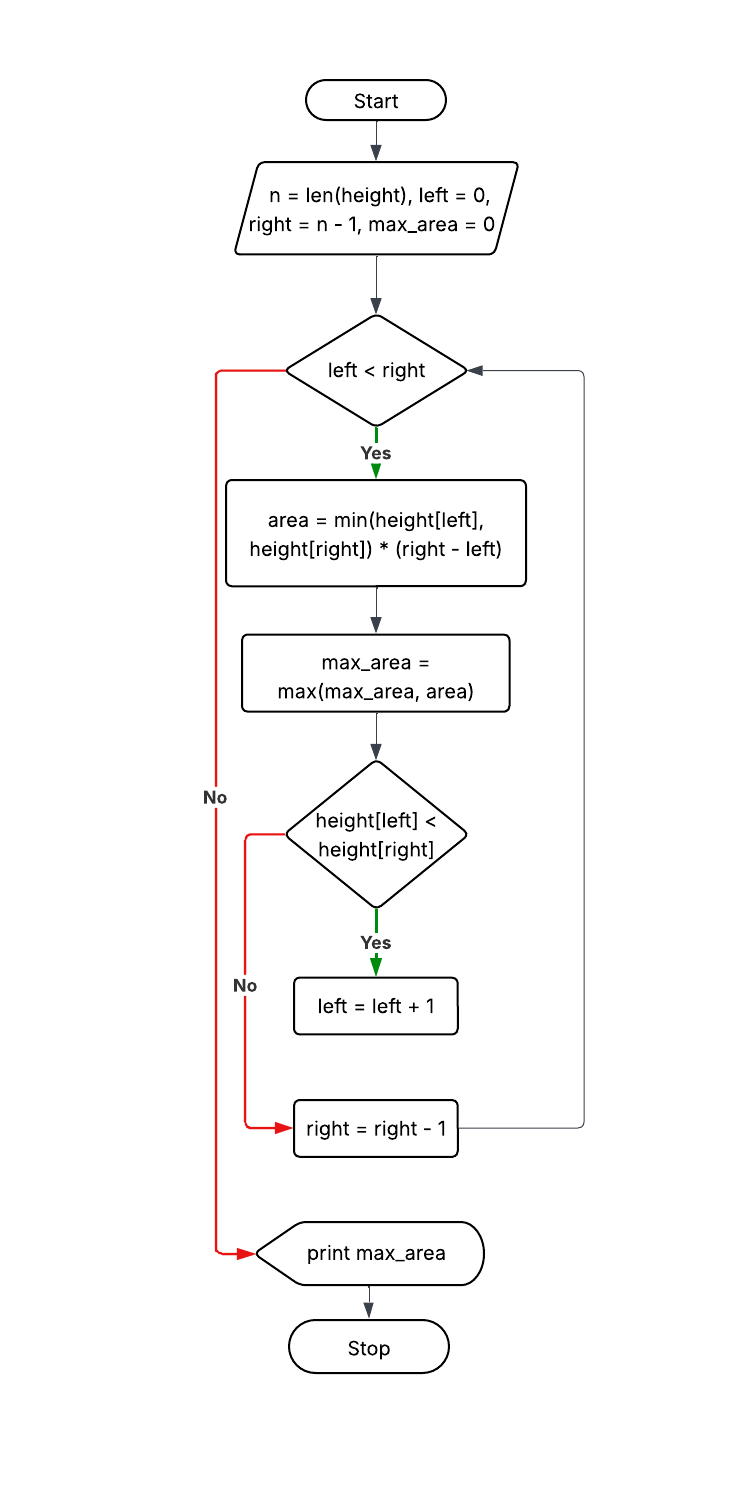
Approach 2: Two Pointers (Optimal)

Explanation: Use two pointers at ends, move the smaller height pointer.

Time: O(n), Space: O(1)

left = 0, right = n-1
max_area = 0
while left < right:
  area = min(height[left], height[right]) * (right - left)
  max_area = max(max_area, area)
  if height[left] < height[right]: left++
  else: right--
return max_area

💡 Think: Can I move pointers inward, dropping the smaller height to find a larger area faster?

Approach 3: Explanation + Visualization

Explanation: Moving the smaller line may increase height without decreasing width too much, ensuring we cover maximum area. This guarantees we find optimal solution in one pass.

Time: O(n), Space: O(1)

same as two-pointer method

💡 Think: What if I shift the shorter line each time, since a taller one might trap more water?

Solve on LeetCode